Dr. Dr. Rudolf Pleier

Interpretationen der Bewertung nach dem Duplikationsprinzip im Mehrperiodenmodell

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

Die ersten drei der nachfolgenden Interpretationen der Bewertung im Mehrperiodenmodell (englisch: multi-period model) liefern Brücken von der Bewertung deterministischer Zahlungsströme zur Bewertung stochastischer Zahlungsströme. Die beiden darauffolgenden Interpretationen der Bewertung von zeitdiskreten Zahlungsströmen in den Abschnitten 4 und 5 findet man auch im zeitkontinuierlichen Marktmodell. Es werden hier die beim Thema ‚Das Mehrperiodenmodell zur Bewertung unsicherer zeitdiskreter Zahlungsströme bei vollkommenem Kapitalmarkt‘ angegebenen Begriffe und Bezeichnungen verwendet.

 

1    Die Bewertung als Abstandsmessung

Bei gültigem Law of One Price (LOP) im Marktmodell stimmen der für die Punkte X ∈ 𝒲 definierte orientierte Abstand  

                                                   d(X) := Ψ^⊤X/||Ψ||

(Ψ ∈ ℳ^⊥ mit Ψ₀ = 1, ||Ψ|| = (Ψ^TΨ)^1/2) von der Hyperebene

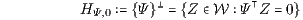
und der für die Zahlungsprofile X = L(h) ∈ L(ℋ_N) definierte Preis

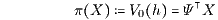
auf L(ℋ_N) bis auf den positiven konstanten Faktor 1/||Ψ|| überein. Die Abstandsfunktion d(X) und die Preisfunktion π(X) liefern daher als Nutzenfunktionen auf L(ℋ_N) die gleiche Präferenzordnung. Somit kann die Bewertung von Zahlungsprofilen X in L(ℋ_N) nach dem Duplikationsprinzip mittels des Startkapitaleinsatzes V₀(h) von Duplikationsstrategien und damit des Preises π(X) wie bei deterministischen Zahlungsströmen auch als Abstandsmessung von einer Hyperebene interpretiert werden. Damit hat man eine erste Brücke von der Bewertung deterministischer zeitdiskreter Zahlungsströme zur Bewertung stochastischer zeitdiskreter Zahlungsströme. In Abbildung 1 ist für ein Zahlungsprofil X = L(h) ∈ L(ℋ_N) der orientierte Abstand d(X) von der Hyperebene H_Ψ,0 und der Beurteilungskurvenpunkt V(μ(X)) dargestellt.

 

2    Die Bewertung als Duplizierung mit einem Supplement vom Kapitalmarkt und der Beurteilungskurve der Sofortentnahme

Bei gültigem Law of One Price (LOP) erhält man für jedes duplizierbare Zahlungsprofil X = L(h) ∈ L(ℋ_N) mit dem nach dem Duplikationsprinzip eindeutig bestimmten Preis

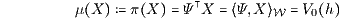
die eindeutig bestimmte Duplizierung

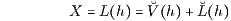
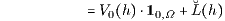
                                             = V(μ(X)) + Z(X) ∈ 𝒱 ⊕ ℳ

mit der Beurteilungskurve V(μ) = μ⋅1_0,Ω = μ⋅(1,0,…,0)^T der Sofortentnahme und dem Supplement (Ergänzungsgeschäft) Z(X) = 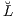(h) vom Kapitalmarkt ℳ = 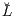(ℋ_N) = L(ker V₀) des Marktmodells. Das Duplizierungskonzept und das Duplikationsprinzip liefern also die gleiche Nutzenfunktion μ(X) = π(X) und die gleiche Präferenzordnung ⊵ auf der Menge L(ℋ_N) der duplizierbaren Zahlungsprofile. Die Bewertung nach dem Konzept der Duplizierung liefert also eine zweite Brücke von der Bewertung deterministischer zeitdiskreter Zahlungsströme zur Bewertung stochastischer zeitdiskreter Zahlungsströme.

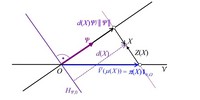
Abb. 1 Die Bewertung des Zahlungsprofils X ∈ L(ℋ_N) durch den orientierten Abstand d(X) von der Hyperebene H_Ψ,0 bzw. durch den Beurteilungskurvenpunkt V(μ(X))  

 

3    Die Bewertung als Diskontierung bzw. Barwertberechnung

3.1 Die Bewertung als Diskontierung der Zahlungen X_t(A_t,k) mittels stochastischer Diskontierungsfaktoren d_t,k

Bei vorausgesetzter Arbitragefreiheit (AF) und Vollständigkeit (VS) des Marktmodells existieren in L(ℋ_N) die Arrow-Debreu-Papiere

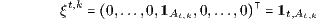∈ 𝒲 = L(ℋ_N)

und im Kapitalmarkt ℳ des Marktmodells die zugehörigen Arrow-Debreu-Kassageschäfte

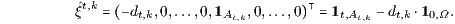
Die hierbei auftretenden und zu den Zeitintervallen [0,t] und Ereignissen A_t,k ∈ 𝒫_t (t ∈ I, k ∈ {1,…,k_t }) gehörigen stochastischen Diskontierungsfaktoren d_t,k = Φ(A_t,k) (Φ ∈ ℳ^⊥ mit Φ > 0 und Φ₀ = 1) stehen auf dem Kapitalmarkt ℳ des Marktmodells in dem Sinne zur Verfügung, dass mit Hilfe des zugehörigen Kapitalmarktgeschäfts 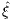^t,k ∈ ℳ eine zum Zeitpunkt t ∈ I und im Ereignis A_t,k ∈ 𝒫_t  stattfindende Zahlung γ =  X_t(A_t,k) ∈ ℝ tatsächlich auf eine gleichwertige sichere Zahlung im Zeitpunkt s = 0 transponiert bzw. abgezinst werden kann: Aus dem Zahlungsprofil

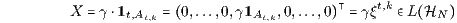
mit dem Preis π(X ) = γπ(ξ^t,k) = γd_t,k erhält man nämlich durch Kombination (additive Ergänzung, Glattstellung, Replizierung) mit dem Kapitalmarktgeschäft Z = - γ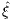^t,k = (γd_t,k,0,…,0,-γ1_At,k,0,…,0) ∈ ℳ das Zahlungsprofil

                         

mit dem gleichen Preis π(Y) = γd_t,k = π(X).   

Für jedes duplizierbare Zahlungsprofil X = L(h) ∈ L(ℋ_N) = 𝒲 erhält man den eindeutig bestimmten Preis

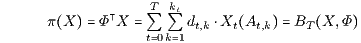
also durch eine spezielle Replizierung, nämlich durch die Diskontierung der Zahlungen X_t(A_t,k) des Zahlungsprofils X mit den stochastischen Diskontierungsfaktoren d_t,k = Φ_t(A_t,k) auf eine gleichwertige sichere Zahlung im Zeitpunkt s = 0. Der Preis π(X) ist also der Barwert B_T(X,Φ) von X, der mit dem stochastischen Ereignispreisvektor

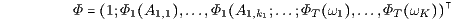
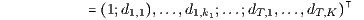
berechnet wird. Diese Bewertung der duplizierbaren stochastischen Zahlungsströme kann als eine vom deterministischen Fall auf den stochastischen Fall verallgemeinerte Diskontierung bzw. verallgemeinerte Barwertberechnung interpretiert werden.

 

3.2 Die Bewertung als Diskontierung der Q_t-Erwartungswerte der Zahlungen X_t bezüglich der Preismaße Q_t mit deterministischen Diskontierungsfaktoren d_t

Unter der Voraussetzung (AF) der Arbitragefreiheit des Marktmodells und der Voraussetzung (DPζ^t) der Duplizierbarkeit der deterministischen Arrow-Debreu-Papiere ζ^t = 1_t = 1_t,Ω = (0,…,0,1,0,…,0)^⊤ für alle t ∈ I erhält man mit einem normierten Zustandsprozess Φ (Φ ∈ ℳ^⊥ ∩ 𝒲_>0 mit Φ > 0 und Φ₀ = 1) für jedes duplizierbare Zahlungsprofil X ∈ L(ℋ_N) den eindeutig bestimmten Preis π(X) durch

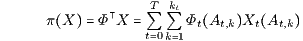
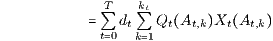
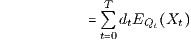
mit den zu den Zeitintervallen [0,t] gehörigen risikolosen (deterministischen) Diskontierungsfaktoren

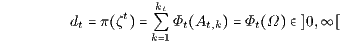
und den zu den Wahrscheinlichkeitsmaßen (W-Maßen) Q_t = Φ_t/d_t gehörigen Erwartungswerten

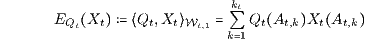
der (Q_t-integrierbaren) ℱ_t-messbaren reellwertigen Zustandsfunktionen X_t. Damit ist der Preis

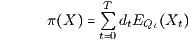
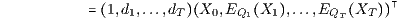
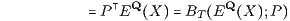
der mit dem deterministischen Preisvektor P = (d₀,…,d_T)^⊤ berechnete Barwert B_T(E^Q(X);P) des deterministischen (T+1)-Tupels

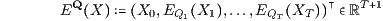
der Q_t-Erwartungswerte E_Qt(X_t) der Zustandsfunktionen X_t. Auch diese Bewertung der duplizierbaren stochastischen Zahlungsströme kann als eine vom deterministischen Fall auf den stochastischen Fall verallgemeinerte Diskontierung bzw. verallgemeinerte Barwertberechnung interpretiert werden.

Abb. 2 Der Preis des Zahlungsprofils X als Barwert der Erwartungswerte der Zustandsfunktionen X_t

 

3.3 Die Bewertung als Diskontierung der Q-Erwartungswerte der Zahlungen X_t bezüglich des Preismaßes Q mit deterministischen Diskontierungsfaktoren d_t

Neben der Arbitragefreiheit (AF) sei jetzt noch die Bedingung (FH), also die Existenz von so genannten festverzinslichen Handelsstrategien vorausgesetzt. Jedes der oben verwendeten W-Maße Q_t : ℱ_t → [0,1] ist dann die Einschränkung Q|_ℱt des W-Maßes Q = Q_T : Ꮘ(Ω) → [0,1] (ℱ_T = Ꮘ(Ω) = Potenzmenge von Ω), des sogenannten (für alle t ∈ I einheitlichen) Preismaßes des Marktmodells, auf die Unter-σ-Algebra ℱ_t ⊆ Ꮘ(Ω). Damit ist nun der Preis π(X) von X ∈ L(ℋ_N) die Summe der mit den risikolosen (deterministischen) Diskontierungsfaktoren d_t diskontierten Q-Erwartungswerte der Zustandsfunktionen X_t bezüglich des im Marktmodell ((S,δ),ℱ) entwickelten Preismaßes Q:

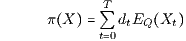
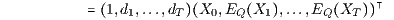
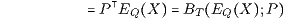
mit dem deterministischen Preisvektor  P = (d₀,…,d_T)^⊤ und dem deterministischen (T+1)-Tupel

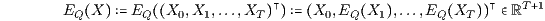
der Q-Erwartungswerte E_Q(X_t) der Zustandsfunktionen X_t bezüglich des Preismaßes Q : Ꮘ(Ω) → [0,1]. Der Preis π(X) des Zahlungsprofils X ist also der mit dem deterministischen Preisvektor P berechnete Barwert B_T(E_Q(X);P) des (T+1)-Tupels E_Q(X) der Q-Erwartungswerte E_Q(X_t) bezüglich des formalen W-Maßes Q auf Ꮘ(Ω). Auch diese Bewertung der duplizierbaren stochastischen Zahlungsströme mittels einer Diskontierung bzw. Barwertberechnung ist eine Verallgemeinerung der entsprechenden Bewertung der duplizierbaren deterministischen Zahlungsströme. Die in den Abschnitten 3.1, 3.2 und 3.3 angegebenen verallgemeinerten Diskontierungen bzw. Barwertberechnungen liefern also weitere Brücken von der Bewertung deterministischer Zahlungsströme zur Bewertung stochastischer Zahlungsströme.

 

4    Die diskontierten Preisprozesse der dividendenlosen Finanzinstrumente sind Martingale bezüglich des Preismaßes Q

Unter Voraussetzung der Arbitragefreiheit (AF) und der Bedingung (FH), also der Existenz von festverzinslichen Handelsstrategien, lässt sich die zum j-ten Finanzinstrument S^j und zum festen Zeitpunkt s gehörige diskontierte Preiszustandsfunktion M_s^j := d_sS_s^j darstellen als Summe der bedingten Erwartung der zu einem festen späteren Zeitpunkt t ≥ s gehörigen diskontierten Preiszustandsfunktion M_t^j = d_tS_t^j und der bedingten Erwartung der diskontierten Dividenden-Zustandsfunktionen γ_i^j := d_iδ_i^j des Zeitintervalls [s+1,t]:

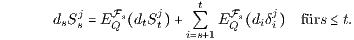
Im Spezialfall eines dividendenlosen Finanzinstruments S^j (δ^j = 0) ist der diskontierte Preisprozess M^j = (M_t^j)_t∈I = (d_tS_t^j)_t∈I ein Martingal bezüglich des W-Maßes Q und der Filtration ℱ = (ℱ_t)_t∈I des gefilterten W-Raums (Ω,ℱ,Q):

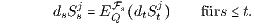
Aufgrund dieser Eigenschaft wird das Preismaß Q auch Martingalmaß genannt. Der Zusammenhang zwischen der Arbitragefreiheit und der Martingaleigenschaft der dividendenlosen diskontierten Preisprozesse wurde im Jahr 1979 von Harrison und Kreps gefunden.

 

5    Die Preisprozesse der dividendenlosen Finanzinstrumente im relativen Marktmodell mit Numéraire sind Martingale bezüglich des Preismaßes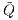

Vorausgesetzt sei nun für das Marktmodell ((S,δ),ℱ) die Arbitragefreiheit (AF) und die Bedingung (NM), dass es ein dividendenloses positives Finanzinstrument S^j gibt und o. B. d. A. der Index j = 1 sei. Für die mit dem Numéraire (Recheneinheit, Bezugsgröße) S¹ diskontierten Preisprozesse (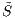_t^j)_t∈I  und diskontierten Dividendenprozesse (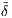_t^j)_t∈I  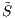(_t^j = S_t^j/S_t¹,  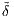_t^j = δ_t^j/S_t¹,  t = 0,…,T,   j = 1,…,N) des relativen (modifizierten, diskontierten) Marktmodells gilt dann die Darstellung:

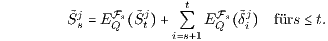
Speziell für die dividendenlosen Preisprozesse S^j (δ^j =0) ist der jeweils zugehörige (mit dem Numéraire S¹ diskontierte) Preisprozess (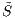_t^j)_t∈I des relativen Marktmodells selbst ein Martingal bezüglich des Preismaßes 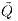des relativen Marktmodells ((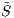,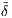),ℱ) und der Filtration ℱ:

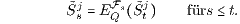
Im arbitragefreien relativen Marktmodell entwickeln sich also die dividendenlosen Preisprozesse (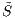_t^j)_t∈I gemäß dem formalen Preismaß 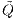wie das Kapital eines Spielers in einem fairen Spiel.

 

Literatur

Jürgen Kremer (2011), Portfoliotheorie, Risikomanagement und die Bewertung von Derivaten, Springer, Berlin Heidelberg. 

Rudolf Pleier (2023), Diskrete stochastische Finanzmathematik, Tredition, Ahrensburg.