Dr. Dr. Rudolf Pleier

Methode des internen Zinssatzes und
Methode der Vielfachheiten der internen Zinsfaktoren

Das Rätsel der Interner Zinssatz-Methode ist gelöst

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

Zu den klassischen Bewertungsmethoden der dynamischen Investitionsrechnung gehört neben der Kapitalwert- (Barwert-), Endwert-, Zeitwert- und Annuitätenmethode auch die Methode des internen Zinssatzes (Interner Zinssatz-Methode, Interner Zinsfuß-Methode, englisch: method of internal rate of return; Abkürzung: MIZ). Diese Methode berechnet zu einem Zahlungsstrom

einen auf die Zinsperioden [k-1,k] (im Allgemeinen Jahre; k = 1,…,n) der Laufzeit n ∈ ℕ bezogenen konstanten und nicht (in Haben- und Sollzinssatz) gespaltenen Zinssatz

einen sogenannten internen Zinssatz des Zahlungsstroms X, und verwendet diesen Zinssatz als Maßstab, um den Zahlungsstron X als vorteilhaft, indifferent (neutral) oder unvorteilhaft zu beurteilen.

Die Bewertung des Zahlungsstroms X erfolgt durch den Vergleich des internen Zinssatzes i_int( X) mit einem vorher festgelegten, für alle Zinsperioden konstanten und nichtgespaltenen Kalkulationszinssatz i_k = i_K > -1 (k = 1,…,n): Es wird geprüft, ob

i_int( X) > i_K, i_int(X) = i_K oder i_int( X) < i_K

ist. Die Bewertung soll dabei konsistent (widerspruchsfrei, im Ergebnis übereinstimmend) zur Kapitalwertmethode (Barwertmethode, Abk.: KWM, BWM) sein, die X als vorteilhaft, indifferent oder unvorteilhaft beurteilt, wenn der mit dem Kalkulationszinsfaktor q_K = 1 + i_K (> 0) berechnete Kapitalwert (Barwert) B_n(X,q_K) von X positiv, gleich Null oder negativ ist:

X ist vorteilhaft      :⇔ B_n(X,q_K) > 0;

X ist indifferent      :⇔ B_n(X,q_K) = 0;

X ist unvorteilhaft  :⇔ B_n(X,q_K) < 0.   

Die Berechnung des internen Zinssatzes erfolgt, indem der zugehörige interne Zinsfaktor q_int = 1 + i_int als eine reellwertige Nullstelle der Endwertfunktion

bzw. als eine von Null verschiedene reellwertige Nullstelle der Barwertfunktion

bestimmt wird. Die Berechnung aller (komplexen) Nullstellen des Polynoms E_n(q) kann bei­spielsweise mittels der Funktion NSolve des Software­systems Mathematica von Wolfram Research erfolgen. Als Zahlungsströme werden nachfolgend ohne Einschränkung nur Investitionen X (X₀ < 0) betrachtet. Für Finanzierungen X (X₀ > 0) erhält man analoge Ergebnisse. 

Nachfolgend werden die folgenden Fragen behandelt:

• Welche Zahlungsströme liegen im Anwendungsbereich von MIZ, d. h. in dem Bereich, in dem die MIZ einen Zahlungsstrom X konsistent zur KWM beurteilt?
• Warum hat die MIZ mit der Verwendung eines einzelnen internen Zinsfaktors bei der Beurteilung eines Zahlungsstroms bzw. beim Vergleich von Zahlungsströmen nur einen eingeschränkten Anwendungsbereich?  
• Gibt es eine Verallgemeinerung der MIZ für die Beurteilung und den Vergleich mit einem größeren Anwendungsbereich?

Das Rätsel der Methode des internen Zinssatzes hinsichtlich ihres eingeschränkten Anwendungsbereichs kann nachfolgend mit nur etwas Basiswis­sen zur Kurvendiskussion für die reellwertige Polynomfunktion E_n(X,q) gelöst werden. Die Lösung ist mathematisch so einfach, dass sich die Frage stellt, warum diese bisher nicht beachtet wurde. Es ist dabei jedoch der sture Blick von einem einzigen internen Zinsfaktor zu lösen und der Blick auf die Gesamtheit der internen Zins­fakto­ren zu richten. Außerdem ist auf die ökonomische Interpretierbarkeit des internen Zinsfaktors q_int als Kontozinsfaktor q_Kto eines Verrechnungskontos für den Zahlungsstrom X zu verzichten. Genau genommen genügt es zur Beurteilung eines Zahlungsstroms im Falle q_K \(\neq\) q_int  die Vielfachheiten der internen Zins­­faktoren q_int zu bestimmen, die größer als der Kalkulationszinsfaktor q_K sind, und zu unterscheiden, ob diese Gesamtvielfachheit ungerade oder gerade ist. Man erhält dann eine Verallgemeinerung der MIZ, die universell auf alle Zahlungsströme anwendbar ist und die äquivalent zu den anderen klassischen Bewertungsmethoden ist. Will man aber an der finanzmathematischen (ökonomischen) Interpretierbarkeit des internen Zinsfaktors q_int  als Kontozinsfaktors q_Kto eines Verrechnungskontos für den Zahlungsstrom X festhalten, so bewirkt dies notwendig die Einschränkung des Anwendungsbereichs auf die Verrechnungskonto-Zahlungsströme. 

 

1    Beurteilung eines einzelnen Zahlungsstroms

1.1 Zahlungsströme mit einem einzigen positiven internen Zinsfaktor ungerader Nullstellenordnung

In der Praxis und der Literatur war es bisher üblich, zur Beurteilung des Zahlungsstroms X mittels MIZ nur einen einzelnen internen Zinsfaktor q_int = q_X zu verwenden. Als interner Zinsfaktor q_int wird dabei die einzige positive Nullstelle der Endwert­funktion E_n(X,q) gewählt. Als Anwendungsbereich der MIZ, auf dem die MIZ konsistent zur KWM ist, werden bisher die Normalinvestitionen, die regulären Investitionen und die sogenannten „isoliert durchführbaren Investitionen“ (siehe Kilger 1965, S. 765ff, Blohm und Lüder 1995, S. 89ff, Götze 2008, S. 97ff) angegeben. Eine derartige Investition X (X₀ < 0) kann dann folgendermaßen beurteilt werden:

                        X ist vorteilhaft        ⇔ B_n(X,q_K) > 0    ⇔ q_int > q_K;    

                        X ist indifferent        ⇔ B_n(X,q_K) = 0    ⇔ q_int = q_K;   

                        X ist unvorteilhaft    ⇔ B_n(X,q_K) < 0    ⇔ q_int < q_K.         

Der Beweis dieser Charakterisierung der KWM-Beurteilung durch die Lagebeziehung von q_int und q_K und auch der nachfolgenden Verallgemeinerungen erfolgt mittels der Nullstellendarstellung und einfacher Kurvendis­kussion für die Polynomfunktion E_n(X,q): Für große q ist die Polynomfunktion E_n(X,q) wegen X₀ < 0 (X Investition) negativ. Demzufolge ist im Falle E_n(X,q_K) ≠ 0 bei ungerader Gesamtordnung der Nullstellen von E_n(X,q) im Intervall ]q_K,∞[ und demnach bei ungerader Anzahl der Nullstellen ungerader Ordnung in ]q_K,∞[ der Endwert E_n(X,q_K) positiv und bei entsprechender gerader Gesamtordnung der Endwert E_n(X,q_K) negativ. Damit wird die Endwertmethode bzw. die Kapitalwertmethode charakterisiert durch die Ungerad- bzw. Geradzahligkeit der Gesamtordnung der internen Zinsfaktoren von X rechts des Kalkulationszinsfaktors q_K. Bei­spiels­weise ist eine Investition X ∈ ℝⁿ⁺¹ genau dann vorteilhaft mit positivem Kapitalwert B_n(X,q_K), wenn diese Gesamtordnung ungerade ist. Die Investition ist genau dann unvorteilhaft mit negativem Kapitalwert B_n(X,q_K), wenn diese Gesamtordnung gerade ist. Ein ausführlicherer Beweis wird beim Thema 'Charakterisierung der Endwertmethode mittels interner Zinsfaktoren' dargestellt.         

Speziell für die „isoliert durchführbaren" Investitionen besitzt der einzige positive interne Zinsfaktor q_int eine besondere Eigenschaft. Er hat einen nichtpositiven Horner-Schema-Vektor

                        E(q_int) = (E₀(q_int),E₁(q_int),…,E_n(q_int))^T   

(mit den Horner-Schema-Polynomen E_j(q) = X₀q^j + X₁q^j-1 + … + X_j-1q + X_j  für j = 0,…,n). Demzufolge ist q_int eine einfache Nullstelle und die einzige positive Vorzeichenwechselstelle. Wegen E(q_int) ≤ O können außerdem die isoliert durchführbaren Investitionen auch als Verrech­nungs­konto-Investitionen (VK-Investitionen) bezeichnet werden, da bei der fiktiven Einzahlung der Investition X auf ein neu angelegtes fiktives Verrechnungskonto (Abk.: VK) mit dem Kreditkontozinsfaktor q_int alle Kontostände C_j = E_j(q_int) nichtpositiv sind und daher keinen Vorzei­chenwechsel aufweisen. Bei den VK-Investitionen kann der positive interne Zinsfaktor q_int also auch ökonomisch als Verrechnungskontozinsfaktor interpretiert werden.

Der Anwendungsbereich der MIZ als Konsistenzbereich von MIZ und KWM kann bei Verwendung eines einzigen positiven internen Zinsfaktors q_int noch auf die NU-Investitionen erweitert werden, für welche q_int die einzige positive Nullstelle der Endwertfunktion E_n(q), von ungerader Ordnung und somit die einzige positive Vorzeichenwechselstelle ist. Eine weitere Erweiterung des Anwendungsbereichs kann noch auf die NF-Investitionen erfolgen, die jeweils keinen positiven internen Zinsfaktor q_int besitzen. Bei der Begründung der Anwendbarkeit der MIZ auf die NU-Investitionen wird aber schon deutlich, dass hierbei die Vielfachheiten der internen Zinsfaktoren eine entscheidende Rolle spielen. Bei der genaueren Untersuchung dieses Gesichtspunkts kann nachfolgend durch eine einfache Verallgemeinerung der MIZ zur MVIZ, der Methode der Vielfachheiten der internen Zinsfaktoren, das Rätsel des eingeschränkten Anwendungsbereichs der MIZ gelöst werden.  

 

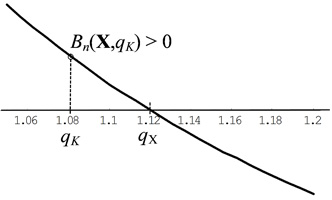
Abb. 1 Der Graph der Barwertfunktion B_n(X,q_K) einer vorteilhaften NU-Investition X mit einem einzigen positiven internen Zinsfaktor q_int = q_X ungerader Nullstellenordnung

 

1.2 Zahlungsströme mit einem einzigen positiven internen Zinsfaktor gerader Nullstellenordnung, mit mehreren verschiedenen positiven internen Zinsfaktoren oder mit keinem positiven internen Zinsfaktor

Um auch für Zahlungsströme mit einem einzigen positiven internen Zinsfaktor, der noch eine gerade Nullstellenordnung aufweist, für Zahlungsströme mit mehreren verschiedenen positiven internen Zinsfaktoren oder mit keinem positiven internen Zinsfaktor eine Beurteilung mittels interner Zinsfaktoren zu erhalten, ist der Blick von einem einzelnen internen Zinsfaktor weg auf die Gesamtheit der internen Zinsfaktoren zu richten, die größer als der Kalkulationszinsfaktor q_K sind. Dazu verwendet man die als Summe der Vielfachheiten definierte Gesamtvielfachheit (Gesamtordnung)

der Nullstellen q_j des Polynoms E_n(X,r) im Intervall ]q_K,∞[. Diese Gesamtvielfachheit derjenigen internen Zinsfaktoren von X, die auf der Zahlengeraden rechts von q_K liegen, wird hier auch kurz als die zu q_K gehörige rechtsseitige Gesamtvielfachheit bezeichnet.

Eine zur KWM äquivalente Methode der Vielfachheiten der internen Zinsfaktoren (Abk.: MVIZ; Methode der internen Zinsfaktoren, Methode der internen Zinssätze), die auf ganz \(\mathbb{R}^{n+1}\) einsetzbar ist,  beurteilt dann eine Investition X (X₀ < 0) folgendermaßen:

 

Abb. 2 Der Graph der Barwertfunktion B_n(X,q_K) einer vorteilhaften Investition X mit ungerader rechtsseitiger Gesamtvielfachheit m_>qK

Als Spezialfälle sind hier die VK-Investitionen (E(q_int) ≤ O) mit einem nichtpositiven internen Zinsfaktor q_int und allgemeiner die Investitionen mit keinem positiven internen Zinsfaktor zu nennen, die bei jedem positiven Kalkulationszinsfaktor q_K als unvorteilhaft beurteilt werden (wegen E_n(X,q) < 0 in ]0,∞[ ist m_>qK = 0 gerade und B_n(X,q_K) < 0 ∀ q_K > 0). Bei den VK-Investitionen mit einem nichtpositiven internen Zinsfaktor q_int kann (wie bei den VK-Investitionen mit positivem internen Zinsfaktor) dieser interne Zinsfaktor q_int auch ökonomisch als Verrechnungskontozinsfaktor interpretiert werden. 

Diese Methode MVIZ ist auch auf Investitionen anwendbar, die allgemeiner als lexikonegative Zahlungsströme definiert sind, bei denen also der erste von Null verschiedene Koeffizient X_k negativ ist. Analog können auch die allgemeiner als lexikopositive Zahlungsströme definierten Finanzierungen bewertet werden. Für den übrig bleibenden Zahlungsstrom X = O ist q_K ein interner Zinsfaktor der Endwertfunktion E_n (O,q) ≡ 0, somit O indifferent und daher auch für diesen Zahlungsstrom die MVIZ-Beurteilung konsistent zur KWM-Beurteilung. Insgesamt sind somit alle Zahlungsströme des ℝⁿ⁺¹ mit der Methode MVIZ konsistent zur KWM beurteilbar.

Warum dieser umfassendere universelle Konsistenzbereich bisher in der Literatur nicht zu finden ist, liegt wohl daran, dass der Blick traditionell starr auf die Verwendung eines einzelnen internen Zinsfaktors gerichtet ist und der interne Zinsfaktor eventuell noch gerne ökonomisch als Kontozinsfaktor eines fiktiven Verrechnungskontos interpretiert werden soll, auf dem der Zahlungsstrom verrechnet wird. Die Forderung dieser ökonomischen Interpretierbarkeit des internen Zinsfaktors führt dann aber zur Einschränkung auf die VK-Zahlungsströme. Richtet man jedoch den Blick auf die Gesamtheit aller internen Zinsfaktoren, so kann schon von einem Gymnasiasten der Oberstufe mittels der Nullstellendarstellung und einfacher Kurvendiskussion für das Polynom E_n(X,q) die KWM mittels der Gesamtvielfachheit m_>qK der internen Zinsfaktoren von X im Intervall ]q_K,∞[ charakterisiert werden.

Die Einschränkung des Anwendungsbereichs von MIZ: Im Gegensatz zur MVIZ liefert jede beliebig definierte Methode "des" internen Zinssatzes (MIZ), die nur einen einzelnen irgend­wie festgelegten internen Zinsfaktor q_int verwendet, nur ei­nen eingeschränkten Anwendungsbereich, d. h. eingeschränkten Konsistenzbereich von MIZ und KWM: In deren Anwendungsbereich gilt dann nämlich beispielsweise auf der Teilmenge der vorteilhaften Inves­titionen X neben der zur KWM-Bedingung B_n(X,q_K) > 0 äquivalenten MVIZ-Bedingung [B_n(X,q_K) ≠ 0 ∧ m_>qK ungerade] noch zusätzlich die MIZ–Zinsfaktor­bedingung an q_int und q_K, wodurch diese Teilmenge eingeschränkt wird. Zur weiteren Verdeutlichung betrachtet man den Fall, dass die NU-Investitionen (mit einzigem positiven internen Zinsfaktor, der noch von unge­rader Ordnung ist) zum Anwendungsbereich gehören und somit die vorteilhaften Investitio­nen durch die Zinsfaktor-Ungleichung q_int > q_K charakterisiert werden. Demzufolge gehört dann eine Inves­tition, die genau einen positiven internen Zinsfaktor q_int besitzt, der noch eine zweifa­che Null­stelle ist und rechts von q_K liegt, nicht zum Anwendungsbereich: Sie wäre nämlich we­gen der Zinsfaktorungleichung q_int > q_K gemäß MIZ vorteilhaft, aber wegen der MVIZ-Be­din­gung [B_n(X,q_K) ≠ 0 ∧ m_>qK gerade] bzw. der Barwertungleichung B_n(X,q_K) < 0 gemäß KWM un­vorteilhaft. Die MIZ ist also im Gegensatz zur MVIZ nicht auf ganz ℝⁿ⁺¹ konsistent zur KWM einsetzbar. 

Das Mysterium des eingeschränkten Anwendungsbereichs von MIZ kann also durch den Übergang zur Methode MVIZ gelöst werden, indem statt eines einzelnen internen Zinsfaktors q_int die Gesamtheit der internen Zinsfaktoren rechts des Kalkulationszinsfaktors q_K zur Charakterisierung der KWM verwendet wird.       

Die Menge der Zahlungsströme außerhalb des Anwendungsbereichs von MIZ: Bei einer irgendwie definierten MIZ mit Verwendung eines einzelnen internen Zinsfaktors q_int können auch die Investitionen ohne (reellen) internen Zinsfaktor mit dem formal hinzugenommenen nichtreellen internen Zinsfaktor q_int := ‑  ∞ für jeden positiven Kalkulationszinsfaktor q_K als unvorteilhafte Investitionen mit im Anwendungsbereich erfasst werden (q_int = ‑ ∞ < q_K und m_>qK = 0, B_n(X,q_K) < 0 ∀ q_K > 0). Die dann verbleibenden nicht im Anwendungsbereich der MIZ liegenden Investitionen X werden genau durch die folgenden drei Fälle beschrieben:  

1. X besitzt q_K als internen Zinsfaktor und noch den für die MIZ-Beurteilung (Vergleich von q_int mit q_K) ausgewählten internen Zinsfaktor q_int ≠ q_K;
2. X mit B_n(X,q_K) > 0 und ungeradem m_>qK besitzt noch den für die MIZ-Beurteilung ausgewählten internen Zinsfaktor q_int ≤ q_K;   
3. X mit B_n(X,q_K) < 0 und geradem m_>qK ≥ 2 besitzt den für die MIZ-Beurteilung ausgewählten internen Zinsfaktor q_int ≥ q_K.        

 

2    Vergleich alternativer Zahlungsströme

Der Vergleich zweier Zahlungsströme X, Y ∈ ℝⁿ⁺¹, X ≠ Y, nach der KWM ist wegen der Linearität der Barwertfunktion B_n(X,q) bezüglich X gleichbedeutend zur Beurteilung des Differenzzahlungsstroms D = X - Y ≠ O:

Wählt man ohne Beschränkung der Allgemeinheit die Reihenfolge von X und Y so, dass D eine Investition (ein lexikonegativer Zahlungsstrom) ist, so ist der KWM-Vergleich von X und Y gleichbedeutend zur Beurteilung von D nach der oben für Investitionen angegebenen Methode MVIZ mit den Vielfachheiten der internen Zinsfaktoren von D. Die Zahlungsströme X, Y ∈ ℝⁿ⁺¹ mit lexikonegativem Differenzzahlungsstrom D = X - Y und der zum Kalkulationszinsfaktor q_K > 0 gehörigen rechtsseitigen Gesamtvielfachheit m_>qK = m_>qK(D)  von D werden nach der MVIZ folgendermaßen verglichen:

X ist ebenso vorteilhaft wie Y :⇔ q_K ist ein interner Zinsfaktor von D;

X ist vorteilhafter als Y            :⇔ q_K ist kein interner Zinsfaktor von D  ∧ ungerade;

X ist unvorteilhaft als Y           :⇔ q_K ist kein interner Zinsfaktor von D   ∧ gerade.

Jede andere Vergleichsmethode, die interne Zinsfaktoren von X und Y (anstelle der internen Zinsfaktoren von D) verwendet, liefert nur einen eingeschränkten Anwendungsbereich: Wählt man nämlich einen Zahlungsstrom X ∈ ℝⁿ⁺¹ mit B_n(X,q_K) ≠ 0, X(λ) :=λ·X für λ ∈ ℝ \ {0} und einen beliebigen weiteren Zahlungsstrom Y ∈ ℝⁿ⁺¹, so kann für das Paar (X(λ),Y) die Barwertdifferenz

durch passende Wahl von λ verschiedene Vorzeichen annehmen. Somit kann für (X(λ),Y) der KWM-Vergleich verschiedene Ergebnisse aufweisen, obwohl die internen Zinsfaktoren von X(λ) und Y und ein Vergleich mittels dieser internen Zinsfaktoren unverändert bleiben. Es gibt also stets Zahlungsstrompaare, für die ein mittels interner Zinsfaktoren von X und Y definierter Vergleich nicht konsistent zum KWM-Vergleich ist.

Ebenso erhält man nur einen eingeschränkten Anwendungsbereich, wenn zum Vergleich von X und Y der Differenzzahlungsstrom D durch den MIZ-Vergleich (Vergleich eines einzelnen internen Zinsfaktors q_int(D) von D mit dem Kalkulationszinsfaktor q_K) beurteilt wird. 

  

3    Beispiele

Beispiel 1. Die Beurteilung eines einzelnen Zahlungsstroms

Für den Zahlungsstrom

              Z = (-100000;+322000;-345600;+123638)^T ∈ ℝ⁴

ergeben sich die internen Zinsfaktoren als Nullstellen der Endwertfunktion E_n(Z,q) mittels der Funktion NSolve des Software­systems Mathematica von Wolfram Research zu

              q₁ = 1,06 und q_2,3 = 1,08.

Bei Verwendung des Kalkulationszinsfaktors q_K = 1,05 ist die rechtsseitige Gesamtvielfachheit m_>qK = 3,

also ungerade und somit die Investition Z nach der MVIZ vorteilhaft.

 

Beispiel 2. Der Vergleich zweier Zahlungsströme

Die Zahlungsströme

              X = (-110000;-58400;+86740;+121660)^T,

              Y = (-100000;-90000;+120000;+110000)^T ∈ ℝ⁴

besitzen den Differenzzahlungsstrom

              D = (-10000;+31600;-33260;+11660)^T ∈ ℝ⁴  

mit den internen Zinsfaktoren

              q₁ = 1,00, q₂ = 1,06 und q₃ = 1,10.

Bei dem Kalkulationszinsfaktor q_K = 1,05 ist für D die rechtsseitige Gesamt­vielfach­heit 

             m_>qK (D) = 2

gerade, somit nach der MVIZ die Investition D = X - Y unvorteilhaft und X unvorteilhafter als Y.

 

4    Rechenaufwand und Kondition der Berechnung der internen Zinsfaktoren

Vergleicht man den Rechenaufwand der Endwertmethode (EWM) oder Barwertmethode (BWM) mit dem der Methode der Viel­fachheiten der internen Zinsfaktoren (MVIZ), so ist es viel einfa­cher nur den Endwert E_n(X,q) oder den Barwert (Kapitalwert) B_n(X,q) = E_n(X,q)/qⁿ an der Stelle des Kalkulationszins­faktors q = q_K zu berechnen als die Gesamtheit der internen Zinsfaktoren zu bestimmen. Bei der im Allgemeinen nötigen iterativen Bestimmung der Nullstellen des Polynom \(E_n(\mathbf{X},r)\) wird von einem Softwaresystem wie z. B. Mathematica von Wolfram Research nämlich intern eine Viel­zahl von Funktions­werten des Polynoms \(E_n(\mathbf{X},r)\) berechnet. Schon hin­sichtlich des Rechenauf­wands bei der praktischen Anwendung wäre also die EWM oder die BWM der MVIZ vorzuziehen.

Weiter kommt dazu, dass die Nullstellenbestimmung für ein Polynom \(E_n(\mathbf{X},r)\) = X₀rⁿ + … + X_n in der Standarddarstellung mit den Ko­effizienten X_j (j = 0,…,n) schlecht konditioniert ist. Dabei können schon einfache Nullstellen schlecht konditioniert sein, während mehrfache Nullstellen stets schlecht konditioniert sind. Dies heißt, dass ein kleiner relativer Fehler in den als Ausgangsdaten vorgegebenen Koeffizienten X_j große relative Fehler in den Rechenresultaten für die Polynomnullstellen bewirkt. Dies kann dann zu einer falschen Bestimmung der Gesamtvielfachheit der reellen Nullstellen im Intervall ]q_K,∞[ und zu einer falschen Beurteilung von X führen. Eine ausführlichere Betrach­tung zur Empfind­lichkeit der Polynomnullstellen in Abhän­gigkeit von den Polynomkoeffizienten findet man bei Stoer (1994), S. 333–335. Ein Zahlenbeispiel zur schlechten Kondition der Berechnung der internen Zinsfaktoren findet man beim Thema ‚Cha­rakterisierung der Endwertmethode mittels interner Zinsfaktoren‘ in der pdf-Datei in Ab­schnitt 3 mit Beispiel 3.

 

5    Äquivalenz der Methode der Vielfachheiten der internen Zinsfaktoren zu den anderen klassischen Methoden

Mit der Bereitstellung von MVIZ ist das Mysterium des eingeschränkten Anwendungsbereichs von MIZ, der Methode „des“ internen Zinssatzes, sowohl für die Beurteilung eines einzelnen Zahlungsstroms als auch für den Vergleich von Zahlungsströmen geklärt und eine Verallgemeinerung von MIZ für alle Zahlungsströme X ∈ ℝⁿ⁺¹ bzw. Zahlungsstrompaare (X,Y) ∈ ℝⁿ⁺¹ × ℝⁿ⁺¹ gleichberechtigt neben die anderen klassischen Methoden (Barwert-, Endwert-, Zeitwert- und Annuitätenmethode) gestellt. Aufgrund der Äquivalenz von MVIZ und KWM ist MVIZ auch zu den anderen klassischen Methoden äquivalent. Die implizite Prämisse für die ökonomische Interpretation dieser Methoden auf ganz ℝⁿ⁺¹ besteht in der realen Verfügbarkeit der Kapitalmarktgeschäfte der Hyperebene

                        H_P(q),0 = {S ∈ ℝⁿ⁺¹ : P(q)^TS = 0}

(mit dem Preisvektor P(q) = (1,1/q,…,1/qⁿ)^T, q = q_K). Unter dieser Voraussetzung kann für den Zahlungsstrom X der Kapitalwert B_n(X,q_K) als eine zum Zeitpunkt t = 0 erfolgende Margenentnahme einer Glattstellung (Replizierung, additiven Ergänzung) mit einem Ergänzungsgeschäft (Supplement) S(X) ∈ H_P(q),0 realisiert werden:

                       X + S(X) = B_n(X,q_K)·e₁ = (B_n(X,q_K),0,...,0)^T.    

Je nach der Beurteilung (vorteilhaft, indifferent oder unvorteilhaft) von X ist der Kapitalwert positiv, Null oder negativ.

In der Praxis kann für einen Entscheider durchaus eine spezielle finanzielle Situation vorliegen, in der zumindest die Zahlungsströme X einer Teilmenge des ℝⁿ⁺¹ tatsächlich mit dem jeweils verfügbaren zugehörigen Supplement S(X) = X - B_n(X,q_K)·e₁ auf ihren Kapitalwert B_n(X,q_K) glattgestellt werden können. Ein Beispiel hierfür wird im Buch des Autors auf S. 260-266 mit Hilfe eines Verrechnungskontos dargestellt.     

Literatur

Blohm Hans und Lüder Klaus (1995), Investition, Vahlen, München, S. 90ff, 8. Auflage.

Götze Uwe (2008), Investitionsrechnung, Springer, Berlin Heidelberg, S. 96–107, 6. Auflage.

Kilger Wolfgang (1965), Zur Kritik am internen Zinsfuß, ZfB Band 35, S. 765-98.

Pleier Rudolf (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage. 

Stoer Josef (1994), Numerische Mathematik 1, Springer, Berlin Heidelberg New York, S. 333-335, 7. Auflage.