Die Vielfalt der Präferenzordnungen nach den Konzepten der Duplizierung und Replizierung zur Beurteilung sicherer diskreter Zahlungsströme bei unvollkommenem Kapitalmarkt
⇒ Das Thema als PDF zum Download
Rudolf Pleier
Juni 2015
Es werden die beim Thema „Die Duplizierung und Replizierung zur Beurteilung von sicheren diskreten Zahlungsströmen“ erklärten Begriffe, Bezeichnungen und Voraussetzungen verwendet. Darüberhinaus tritt jetzt noch der Begriff der P-Äquivalenz ~P und L-Äquivalenz ~L von zwei Parameterdarstellungen W(μ) und W′(μ) von Beurteilungskurven auf:
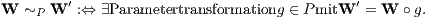
Dabei ist P die Menge aller streng monoton steigenden, surjektiven und stetigen Funktionen g : J′→ J zu beliebigen Intervallen J′, J ⊆ ℝ.

Hierbei ist CMn die aus dem Supplementsystem L (Definition siehe unten in Satz 2) gebildete zulässige Supplementmenge und S′(Y0) das voraussetzungsgemäß eindeutig bestimmte Supplement bei der Duplizierung von Y0 bezüglich der Beurteilungskurve W′(μ):
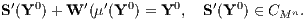
Die Abhängigkeit der mittels der Konzepte der Duplizierung (Nachbildung, additiven Zerlegung) und Replizierung (Glattstellung, additiven Ergänzung) erhaltenen D- und R-Präferenzordnungen von dem Supplementsystem L und von der Beurteilungskurve W(μ) wird in den beiden folgenden mathematischen Sätzen über die Vielfalt der D- und R-Präferenzordnungen beschrieben.
Satz 1 Die Vielfalt der D-Präferenzordnungen bzw. R-Präferenzordnungen in Abhängigkeit vom Supplementsystem
Es liege ein Kapitalmarkt vor, bei dem die Menge K ⊆ ℝn+1 der Kapitalmarktgeschäfte ein konvexer linearer Kegel ist. In K werden zwei Supplementsysteme L und L* betrachtet, für welche jeweils in Verbindung mit der Beurteilungskurve W(μ) die Existenz und Einzigkeit der Duplizierung bzw. der Replizierung für jeden Zahlungsstrom X ∈ ℝn+1 gesichert ist. Die beiden zugehörigen D-Präferenzordnungen bzw. R-Präferenzordnungen stimmen genau dann überein, wenn die beiden zulässigen Supplementmengen gleich sind:
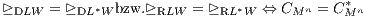 .
.
Satz 2 Die Vielfalt der D-Präferenzordnungen bzw. R-Präferenzordnungen in Abhängigkeit von der Beurteilungskurve
Es liege ein Kapitalmarkt vor, bei dem die Menge K ⊊ ℝn+1 der Kapitalmarktgeschäfte ein konvexer linearer Kegel ist, der keine Arbitragegelegenheit S ∈ {X ∈ ℝn+1 : X ≥ O ∧ X ≠ O} enthält:
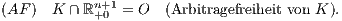
In der Menge K soll ein Supplementsystem
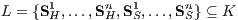
aus n Investitionen SjH und n Finanzierungen SjS (j = 1,…,n) existieren, für welches jedes der 2n n-Tupel
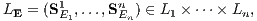
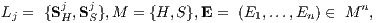
von Kapitalmarktgeschäften SjEj des Systems L aus n linear unabhängigen Zahlungsströmen besteht. Weiter soll die als Vereinigung der Transformationskegel
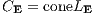
gebildete zulässige Supplementmenge, der gesamte Transformationskegel,
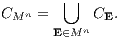
zusammen mit der jeweils verwendeten homogenen Beurteilungskurve
![V : μ ∈ J = ]a,b[ ↦→ V (μ) ∈ ℝn+1](/Media/images/Themen/Thema02/Formeln/wst210x.png)
den gesamten Raum ℝn+1 aufspannen:
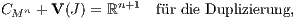
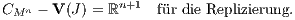
Bei der Replizierung ist noch ein beliebiger Basiszahlungsstrom B ∈ ℝn+1 fest vorgegeben. Die dadurch für jeden Zahlungsstrom X ∈ ℝn+1 mögliche Duplizierung bzw. Replizierung mittels zulässiger Supplementmenge CMn und inhomogener Beurteilungskurve
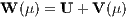
soll jeweils nur auf eine einzige Weise möglich sein. Zur Beschreibung der Vielfalt der mit den Konzepten der Duplizierung und Replizierung definierten D-Präferenzordnungen ⊵DW und R-Präferenzordnungen ⊵RW in Abhängigkeit von der Beurteilungskurve werden drei Fälle unterschieden:
a) Im Fall (LV) eines vollkommenen Supplementsystems L (-L ⊆ K) existiert ein positiver Normalenvektor P ∈ V⊥ (V = K ∩ (-K)), so dass die Menge K der Kapitalmarktgeschäfte im abgeschlossenen homogenen Halbraum HP,0≤ liegt:
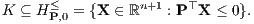
Genauer ist dabei die Menge K der Kapitalmarktgeschäfte im Falle eines vollkommenen Kapitalmarkts gleich der Hyperebene HP,0 und im Falle eines unvollkommenen Kapitalmarkts gleich dem Halbraum HP,0≤. In beiden Fällen stimmen sämtliche D- und R-Präferenzordnungen mit der B-Präferenzordnung ⊵ überein, welche die Zahlungsströme X ∈ ℝn+1 mittels ihrer Barwerte Bn(X) = P⊤X vergleicht. Es gibt also genau eine L-Äquivalenzklasse, die alle Parameterdarstellungen von Beurteilungskurven enthält, und genau eine D- bzw. R-Präferenzordnung. Für alle Parameterdarstellungen W(μ) und W′(μ) von Beurteilungskurven gilt also
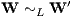
und für alle D-Präferenzordnungen ⊵DW, ⊵DW′ und alle R-Präferenzordnungen ⊵RW, ⊵RW′ gilt

b) Im Fall (LU) eines streng unvollkommenen Supplementsystems L (-L ⊆ ∁K = ℝn+1 \ K) gehören zu verschiedenen Beurteilungskurven W und W′, die als P-Äquivalenzklassen verschieden sind bzw. die verschiedene Spuren besitzen, auch verschiedene R-Präferenzordnungen ⊵RW und ⊵RW′ und verschiedene D-Präferenzordnungen ⊵DW und ⊵DW′. Somit gibt es genau so viele R-Präferenzordnungen bzw. D-Präferenzordnungen wie es Beurteilungskurven gibt. Jede L-Äquivalenzklasse von Parameterdarstellungen stimmt mit einer P-Äquivalenzklasse von Parameterdarstellungen der Beurteilungskurven überein. Für alle Parameterdarstellungen W(μ) und W′(μ) von Beurteilungskurven gilt also
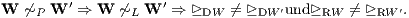
c) Im Fall (LS) eines schwach unvollkommenen Supplementsystems L (-L ∩ K ≠ ∅ ∧ - L ∩ ∁K ≠ ∅) und auch allgemein im Fall eines beliebigen Supplementsystems gehören zu zwei Parameterdarstellungen W(μ) und W′(μ) von Beurteilungskurven genau dann gleiche R-Präferenzordnungen ⊵RW und ⊵RW′ bzw. gleiche D-Präferenzordnungen ⊵DW und ⊵DW′, wenn die Parameterdarstellungen L-äquivalent sind:
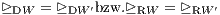
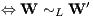
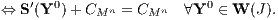
Es gibt also genau so viele D-Präferenzordnungen bzw. genau so viele R-Präferenzordnungen, wie es L-Äquivalenzklassen von Parameterdarstellungen der Beurteilungskurven gibt.
Die Abbildung 1 zeigt zwei L-äquivalente Beurteilungskurven W(μ) und W′(μ) bei einem unvollkommenen Supplementsystem L mit nichttrivialem Linienkegel RMn = CMn ∩ (-CMn).
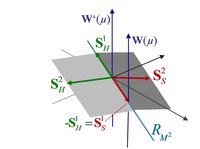
Abb. 1 Zwei L-äquivalente Beurteilungskurven W(μ) und W′(μ) bei einem unvollkommenen Supplementsystem L für die Laufzeit n = 2
Literatur
Rudolf Pleier (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage.