Die Duplikation als Zahlungsprofil einer Handelsstrategie zur Beurteilung unsicherer diskreter Zahlungsströme bei vollkommenem Kapitalmarkt
⇒ Das Thema als PDF zum Download
Rudolf Pleier
Juni 2015
Nachfolgend werden die beim Thema ‚Das Mehrperiodenmodell zur Beurteilung unsicherer Zahlungsströme bei vollkommenem Kapitalmarkt‘ angegebenen Begriffe und Bezeichnungen verwendet. Zur Bewertung mittels des Marktmodells ((S,δ),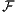
) sind nur Zahlungsströme
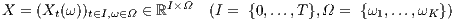
im Vektorraum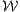 
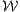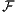= 1() der 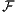-adaptierten reellwertigen stochastischen Prozesse zugelassen. Außerdem soll die Bewertung nach dem Duplikationsprinzip („Pricing by Duplication“) erfolgen, bei dem das zu bewertende Zahlungsprofil X ∈ 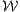als das Zahlungsprofil
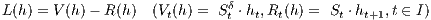
einer Handelsstrategie h ∈
N dupliziert (nachgebildet, erreicht) werden kann. Die Übereinstimmung der beiden Zahlungsprofile X und L(h) soll dabei für alle t ∈ I und ω ∈ Ω gelten, also insbesondere sicher bezüglich der Eintrittswahrscheinlichkeiten der Kursentwicklungen. Eine Duplikationsstrategie h ∈ L-1({X}) von X kann dann sicher und linearalgebraisch durch das Lösen des gestaffelten inhomogenen linearen Gleichungssystems
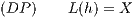
bestimmt werden. Die Gleichung (DP) stellt für die Komponenten htj(At-1,k) (j = 1,…,N) der Zustandsfunktionswerte ht(At-1,k) = (ht1(At-1,k),…,htN(At-1,k))⊤ der Handelsstrategie h ein gestaffeltes lineares Gleichungssystem dar:
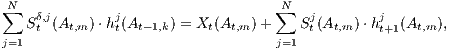
hT+1 = 0, t ∈{T,T-1, …,0}, k ∈ {1,…,kt-1}, m ∈{1,…,kt} mit At,m ⊆ At-1,k. Beispielsweise erhält man für t = 1 das Gleichungssystem
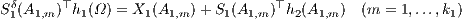
aus k1 Gleichungen für die N Unbekannten h1j(Ω) (j = 1,…,N). Für t = 0 erhält man die einzige Gleichung
für die Berechnung der N Unbekannten h0j(Ω) (j = 1,…,N) oder für die unmittelbare Berechnung des Vermögenswertes
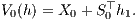
Falls noch der Portfoliowert V0(h) bei t = 0 für alle Duplikationsstrategien h von X konstant ist, kann der Preis π(X) von X bzw. der Wert von X zum Zeitpunkt t = 0 durch den deterministischen Startkapitaleinsatz V0(h) = S0δ(Ω)⊤h0(Ω) der Handelsstrategie h zum Zeitpunkt t = 0 definiert werden:
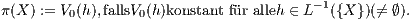
Falls zumindest für ein X ∈ L(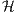N) diese Eigenschaft erfüllt ist, dass also V0(h) konstant für alle h ∈ L-1({X}) ist, so kann gezeigt werden, dass diese Eigenschaft dann auch für alle X ∈ L(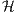N) vorliegt. Im Unterraum L(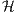N) (⊆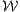) der duplizierbaren Zahlungsprofile des Marktmodells ((S,δ),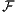) gilt dann das so genannte Gesetz des eindeutig bestimmten Preises (englisch: Law of One Price, Abk.: LOP). Bei Gültigkeit des LOP kann der Preis π(X) eines Zahlungsprofils X ∈ L(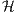N) auch noch ohne die Berechnung einer Duplikationsstrategie h ∈ L-1({X}) mit dem (normierten) Bewertungsprozess Ψ ∈ L*-1({b}) ⊆ 
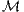⊥ \ ker L* (Ψ0 = 1) als das Skalarprodukt von Ψ und X bestimmt werden (siehe Thema ‚Das Mehrperiodenmodell zur Bewertung unsicherer Zahlungsströme bei vollkommenem Kapitalmarkt‘):
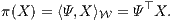
Wie beim Thema ‚Interpretationen der Bewertung nach dem Duplikationsprinzip im Mehrperiodenmodell‘ dargestellt wird, kann diese Duplikation von X mittels einer Handelsstrategie h ∈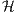N auch als Duplizierung mit der Beurteilungskurve V(μ) = μ ⋅ (1,0,…,0)⊤ = μ ⋅ 10,Ω der Sofortentnahme und einem Supplement (Ergänzungsgeschäft) Z(X) vom Kapitalmarkt 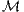= L(ker V 0) = 
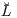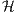(N) des Marktmodells gedeutet werden. Weitere Interpretationen der Bewertung nach dem Duplikationsprinzip werden noch durch drei Arten von verallgemeinerten Diskontierungen gegeben. Die Abbildung 1 zeigt die Duplikation eines Zahlungsprofils X durch das Zahlungsprofil L(h) einer Handelsstrategie h.
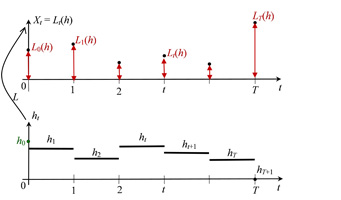
Abb. 1 Die Duplikation eines Zahlungsprofils X mittels des Zahlungsprofils L(h) einer Handelsstrategie h (N = 1)
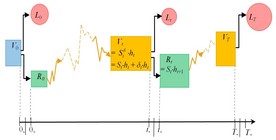
Abb. 2 Die Präzisierung der zeitlichen Entwicklung des Portfoliowerts mittels Vermögenswert Vt(h), Reinvestitionswert Rt(h) und Portfolioauszahlung Lt(h) zum Zeitpunkt t