Dr. Dr. Rudolf Pleier

Charakterisierung der Übereinstimmung von Endwert- und Barwert-Präferenzordnung bei gespaltenen Auf- und Abzinsungsfaktoren

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

1 Der Endwert und der Barwert eines Zahlungsstroms

Der Endwert E_n(X) des Zahlungsstroms X = (X₀,…,X_n)^⊤ ∈ ℝⁿ⁺¹ kann statt mit einem konstanten Kalkulationszinsfaktor allgemeiner mit fristigkeitsabhängigen Haben- und Soll-Aufzinsungsfaktoren a_j,n,Dj(X) folgendermaßen definiert werden:

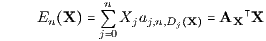
mit dem orthantenweise konstanten Aufzinsungsvektor

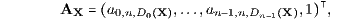
den für die Intervalle [j,n] vorgegebenen Aufzinsungsfaktoren a_j,n,Dj(X) > 0 (j = 0,…,n; a_n,n,D := 1 für D = H, S und dem j-ten Zinssatztypindex

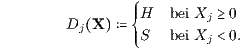
Eine Plausibilisierung für die Definition des Zinssatztypindexes D_j(X) bei den Aufzinsungs­faktoren findet man bei Pleier (2021), S. 212, mittels eines Ergänzungsgeschäfts in Form einer Investition oder Finanzierung.

 

Der Barwert (Kapitalwert, Kapitalgegenwartswert, Gegenwartswert, englisch: present value; bei Zahlungsströmen aus Einnahmen und Ausgaben, also mit Vorzeichenwechsel, auch Nettobarwert, englisch: netto present value) B_n(X) des Zahlungsstroms X = (X₀,…,X_n)^⊤ ∈ ℝⁿ⁺¹ wird mit fristigkeitsabhängigen Haben- und Soll-Abzinsungsfaktoren (Diskontierungsfaktoren) d_0,j,Fj(X) folgendermaßen definiert:

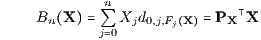
mit dem orthantenweise konstanten Abzinsungsvektor (Diskontierungsvektor)

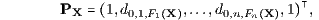
den für die Intervalle [0,j] vorgegebenen Abzinsungsfaktoren d_0,j,Fj(X) > 0 (j = 0,…,n; d_0,0,D := 1 für D = H, S und dem j-ten Zinssatztypindex

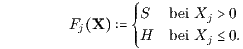
Eine Plausibilisierung für die Definition des Zinssatztypindexes F_j(X) bei den Abzinsungs­faktoren findet man bei Pleier (2021), S. 218, mittels eines Ergänzungsgeschäfts in Form einer Finanzierung oder Investition.         

 

2 Die ökonomische Interpretation des Endwerts und Barwerts jeweils als Margenwert einer Replizierung

Der Endwert E_n(X) ist die Endentnahme (der Margenendwert) ν(X) zum Zeitpunkt t = n bei einer speziellen Replizierung (Glattstellung) des Zahlungsstroms X,

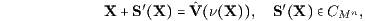
nämlich bei der Replizierung mit dem Basiszahlungsstrom B = O, dem Bezugszahlungsstrom U = O, der Beurteilungskurve

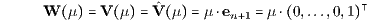
der Endentnahme und einem speziellen Supplementsystem L = L(R^j_Ej ) von Termingeschäften S^j_H = R^j_H, S^j_S = - R^j_S  (j = 1,…,n) mit den elementaren Zahlungsströmen

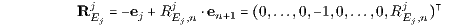
und den Komponenten R^j_Ej,k = 0 für k ≠ j-1, n,  R^j_Ej,j-1 = -1 für k = j-1 und R^j_Ej,n = a_j-1,n,Ej > 0 für k = n (j = 1,…,n, E_j ∈ M = {H,S}).

Der Barwert (Kapitalwert) B_n(X) ist die Sofortentnahme (der Margenbarwert) ν(X) zum Zeitpunkt t = 0 bei einer speziellen Replizierung des Zahlungsstroms X,

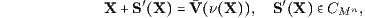
nämlich bei der Replizierung mit dem Basiszahlungsstrom B = O, dem Bezugszahlungsstrom U = O, der Beurteilungskurve

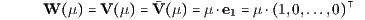
der Sofortentnahme und einem speziellen Supplementsystem L = L(K^j_Ej ) von Kassageschäften S^j_H = K^j_H, S^j_S = - K^j_S  (j = 1,…,n) mit den elementaren Zahlungsströmen

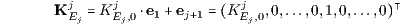
und den Komponenten K^j_Ej,0 = - d_0,j,Ej < 0 für k = 0, K^j_Ej,k = 0 für k ≠ 0, j  und K^j_Ej,j = 1 für k = j  (j = 1,…,n, E_j ∈ M = {H,S}).

Die implizite Prämisse einer ökonomischen Interpretation der Zeitwertmethode bzw. des Zeitwerts Z_m,n(X) zum Zeitpunkt t = m (insbesondere des Endwerts mit m = n und des Barwerts mit m = 0) für den fest fixierten Zahlungsstrom X besteht in der Forderung der realen Verfügbarkeit des speziellen Kapitalmarktgeschäfts S‘(X) auf dem Kapitalmarkt K:

\(\mathbf{S'}(\mathbf{X}) = \text{- } \mathbf{X} + Z_{m,n}(\mathbf{X})\mathbf{e}_{m+1} \in K. \)

In der nachfolgenden Charakterisierung der Übereinstimmung von Barwert- und Endwert-Präferenzordnung wird die zu einem Supplementsystem L gehörige zulässige Supplementmenge C_Mⁿ verwendet:

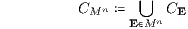
mit den konvexen linearen Kegeln C_E := cone L_E = {S = L_Eλ : λ ≥ O},  L_E = (S¹_E1,…,Sⁿ_En) ∈ L₁ ×...× L_n, L_j = {S^j_H,S^j_S }, E ∈ Mⁿ.

Die nachfolgende Abbildung 1 gehört zu einem Beispiel für n = 2, bei dem die Barwert- und die Endwert-Präferenzordnung übereinstimmen und die gemeinsame zulässige Supplementmenge C_Mⁿ = C'_Mⁿ unvollkommen ist, also verschieden von einer Hyperebene H_T,0 ist. Dabei wird auch der Linien(doppel)kegel \(R_{M^n}\) dargestellt, der eine wichtige Rolle spielt bei der Untersuchung der Vielfalt der mittels Duplizierung und Replizierung erzeugten D- und R-Präferenzordnungen:

\(R_{M^n} := C_{M^n} \cap (\text{- }C_{M^n}) .\)

 

3 Die Übereinstimmung von Endwert- und Barwert-Präferenzordnung

Für den zum Supplementsystem L = L(R^j_Ej ) gebildeten fiktiven Kapitalmarkt

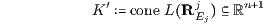
sei die Arbitragefreiheit

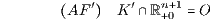
vorausgesetzt, die durch die Ungleichungen

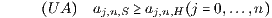
für die Aufzinsungsfaktoren charakterisiert wird. Die zu den Vergleichszeitpunkten m = 0 und m = n gehörige Barwert-Präferenzordnung ≽_B und Endwert-Präferenzordnung ≽_E stimmen genau dann überein, wenn die beiden folgenden Bedingungen erfüllt sind:

1) Die zu den Supplementsystemen  L = L(K^j_Ej ) und L' = L(R^j_Ej ) gehörigen zulässigen Supplementmengen C_Mⁿ = C_Mⁿ(L) und C '_Mⁿ = C_Mⁿ(L') stimmen überein.

2) Der zu den beiden Vergleichszeitpunkten m = 0 und m = n gehörige Aufzinsungsfaktor a_0,n,D0 ist kein gespaltener Aufzinsungsfaktor, d. h. es stimmen der Haben- und der Soll-Aufzinsungsfaktor überein:

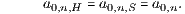
Eine gleichwertige Bedingung ist

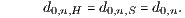
Dies ist die Aussage von Zusatz 6.2 im unten angegebenen Buch ‚Finanzmathematik‘ auf Seite 245f.

 

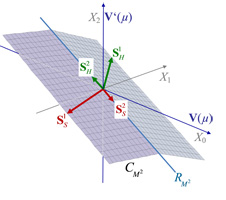
Abb. 1 Die zulässige Supplementmenge \(C_{M^2}\) und der Linienkegel \(R_{M^2}\)  der übereinstimmenden Barwert- und Endwert-Präferenzordnung für die Laufzeit n = 2 bei gespaltenem Auf- und Abzinsungsfaktor der Zinsperiode [0,1]

 

Im Spezialfall von nichtgespaltenen Auf- und Abzinsungsfaktoren stimmen die Barwert- und die Endwert-Präferenzordnung genau dann überein, wenn der Abzinsungsvektor T⁰ = (d_0,0,…,d_0,n)^⊤ (d_0,0 = 1) und der Aufzinsungsvektor Tⁿ = (a_0,0,…,a_n,n)^⊤ (a_n,n = 1) sich nur um einen positiven konstanten Faktor unterscheiden: Tⁿ = \(\delta\)T⁰ mit \(\delta\) > 0. Dies ist die Aussage von Zusatz 6.3 im Buch ‚Finanzmathematik‘ auf Seite 246-247.

 

Literatur

Rudolf Pleier (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage.