Dr. Dr. Rudolf Pleier

Ein Alternativsatz über die Disjunktheit punktierter konvexer Kegel

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

Mittels des Trennungssatzes von Eidelheit (benannt nach dem polnischen Mathematiker Meier Eidelheit, 1910–1943), nach dem ein nichtleerer abgeschlossener konvexer linearer Kegel und eine nichtleere kompakte konvexe Menge im Falle ihrer Disjunktheit durch eine affine Hyperebene strikt getrennt werden können, kann der folgende Alternativsatz über die Disjunktheit punktierter konvexer Kegel bewiesen werden. Der Teil b) dieses Satzes, in dem der konvexe lineare Kegel speziell ein linearer Unterraum ist, steht im engen Zusammenhang mit dem Satz von Stiemke (benannt nach dem deutschen Mathematiker Erich Stiemke, 1892–1915) und dem Minkowski-Farkas-Lemma (benannt nach dem ungarischen Physiker und Mathematiker Julius Farkas, 1847–1930, und dem deutschen Mathematiker und Physiker Hermann Minkowski, 1864–1909).

Mit ihm kann sowohl für den deterministischen als auch für den stochastischen Fall eines arbitragefreien vollkommenen Kapitalmarkts für den Unterraum der Kapitalmarktgeschäfte die Existenz eines strikt positiven Normalenvektors, des sog. Preisvektors P bzw. Diskontierungsprozesses (Zustandspreisprozesses) Φ, nachgewiesen werden. Indem für den Unterraum T der Unterraum der Kapitalmarktgeschäfte gesetzt wird, liefert der Satz unmittelbar den Fundamentalsatz der Preistheorie für das Mehrperiodenmodell: Die Arbitragefreiheit ist äquivalent zur Existenz eines positiven Preisvektors bzw. Diskontierungsprozesses. Bei deterministischem unvollkommenen Kapitalmarkt kann die Existenz eines positiven Normalenvektors P nur für den Linienraum der vollkommenen Kapitalmarktgeschäfte und nicht für den gesamten (im Allgemeinen nicht topologisch abgeschlossenen) Kegel der Kapitalmarktgeschäfte gefolgert werden.

Beweise für den nachfolgenden Satz, einer Verallgemeinerung des Satzes, die Zu­sätze und den Vergleich der inhomogenen Version des Satzes von Stiemke mit dem Minkowski-Farkas-Lemma findet man im Buch des Autors auf S. 389, 395-400 und bei den Download-Themen auf dieser Autorenwebsite www.pleier-r.de.

 

Satz 1  Alternativsatz über die Disjunktheit punktierter konvexer Kegel

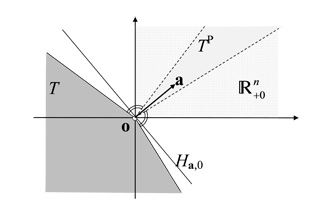
a) Der nichtleere abgeschlossene konvexe lineare Kegel T ⊆ ℝⁿ und der punktierte nichtnegative Orthant

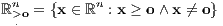
sind genau dann disjunkt, wenn es einen (strikt) positiven Vektor a im polaren Kegel

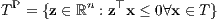
von T gibt und somit T in einem abgeschlossenen homogenen Halbraum

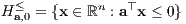
und im offenen homogenen Halbraum

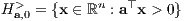
mit positivem Normalenvektor a liegt:

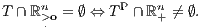
Der Satz lässt sich auch als Alternativsatz formulieren: Es hat also entweder T mit dem punktierten nichtnegativen Orthanten  einen leeren Durchschnitt oder T^P mit dem (strikt) positiven Orthanten

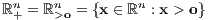
einen leeren Durchschnitt.

Eine äquivalente Formulierung lautet: Es hat entweder T mit dem punktierten nichtnegativen Orthanten einen nichtleeren Durchschnitt oder es besitzt T^P mit dem positiven Orthanten einen nichtleeren Durchschnitt. Von den beiden folgenden Aussagen gilt also entweder (1) oder (2):

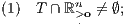
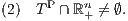
b) Der lineare Unterraum T ⊆ ℝⁿ und der punktierte nichtnegative Orthant sind genau dann disjunkt, wenn einen positiven Vektor a im orthogonalen Komplement T^⊥ gibt und somit T in einer homogenen Hyperebene

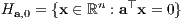
und im offenen homogenen Halbraum mit positivem Normalenvektor a liegt:

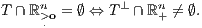
Von den beiden folgenden Aussagen gilt also entweder (1) oder (2):

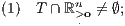
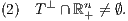
a)

b)

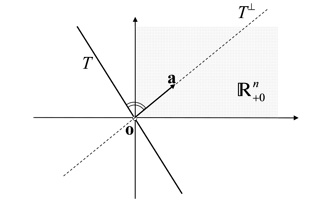Abb. 1 Ein abgeschlossener konvexer linearer Kegel T und ein linearer Unterraum T, die jeweils zum punktierten nichtnegativen Orthanten disjunkt sind, und ein positiver Vektor a ∈ T^P bzw. T^⊥

 

Zusatz 2  Disjunktheit einer Hyperebene und des schwach positiven Orthanten

Die lineare Hyperebene H_a,0 und der schwach positive (punktierte nichtnegative) Orthant sind genau dann disjunkt, wenn es einen positiven (oder negativen) Normalenvektor a der Hyperebene gibt. Bei positiv gewähltem Normalenvektor a der Hyperebene H_a,0 liegt der schwach positive Orthant im offenen homogenen Halbraum :  

 

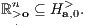
Beschränkt man sich in Satz 1, Teil a) auf abgeschlossene konvexe lineare Kegel T, die als Durchschnitt von endlich vielen homogenen Halbräumen gebildet werden, also auf polyedrische Kegel, bzw. nach dem Polyederdarstellungssatz gleichbedeutend dazu auf endlich erzeugte lineare Kegel, so kann dessen Aussage in einen Alternativsatz über die Lösbarkeit endlicher linearer Ungleichungssysteme umformuliert werden. Ebenso liefert Satz 1, Teil b) einen entsprechenden Alternativsatz, da ein linearer Unterraum T ⊆ ℝⁿ stets als Durchschnitt endlich vieler linearer Hyperebenen bzw. als Lösungsraum eines homogenen linearen Gleichungssystems und auch als lineare Hülle einer Basis von T dargestellt werden kann.

 

Zusatz 3  Alternativsatz über die Lösbarkeit von homogenen linearen Ungleichungssystemen

Es sei die Matrix L ∈ ℝ^n×m gegeben.

a) Von den beiden folgenden Ungleichungssystemen ist dann entweder (1‘) oder (2‘) lösbar:

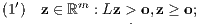
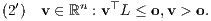
b) Satz der Alternativen von Erich Stiemke (1915): Von den beiden folgenden Ungleichungssystemen ist dann entweder (1‘) oder (2‘) lösbar:

 

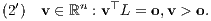
Den entsprechenden Satz über inhomogene lineare Ungleichungssysteme erhält man mittels einer Variablentransformation mit den Matrizen

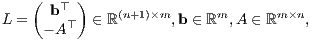
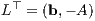
und den Variablen

 

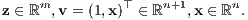
Zusatz 4  Alternativsatz über die Lösbarkeit von inhomogenen linearen Ungleichungssystemen

Es sei eine Matrix A ∈ ℝ^m×n und ein Vektor b ∈ ℝ^m gegeben.

a) Es ist dann genau eines der beiden folgenden Ungleichungssysteme (1”) oder (2”) lösbar:

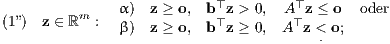
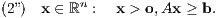
b) Inhomogene Version des Satzes von Stiemke: Es ist dann genau eines der beiden folgenden Ungleichungssysteme (1”) oder (2”) lösbar:

 

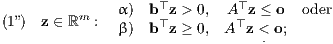
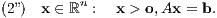
Der Vergleich der inhomogenen Version des Satzes von Stiemke mit dem Minkowski-Farkas-Lemma

Das Minkowski-Farkas-Lemma besagt, dass für eine Matrix A ∈ ℝ^m×n und einen Vektor b ∈ ℝ^m genau eines der beiden folgenden Ungleichungssysteme (I) oder (II) lösbar ist:

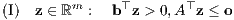
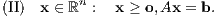
Im Ungleichungssystem (II) wird mit den nichtnegativen x eine größere Lösungsmenge zugelassen als im Ungleichungssystem (2”) der inhomogenen Version des Satzes von Stiemke mit den positiven x. Im Gegenzug dazu verkleinert sich in (I) die Lösungsmenge auf den Fall α) von (1”). Beim Ungleichungssystem (I) des Minkowski-Farkas-Lemmas wird für die schwache Positivität des Vektors Lz = (b^⊤z,-A^⊤z)^⊤ im Ungleichungssystem (1”) also nur der Fall α) und nicht auch noch der Fall β) zugelassen.

Das Minkowski-Farkas-Lemma bedeutet geometrisch, dass der Vektor b ∈  ℝ^m entweder gemäß (II) in dem von den Spalten a_j ∈ ℝ^m der Matrix A = (a₁,…,a_n) erzeugten konvexen linearen Kegel liegt,

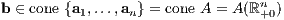
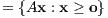
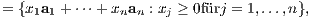
oder gemäß (I) sich von diesem Kegel folgendermaßen trennen lässt (siehe Abbildung 2):

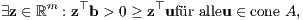
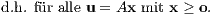
Eine Begründung für diese geometrische Interpretation findet man im unten angegebenen Buch ‚Finanzmathematik‘ auf S. 617–620 oder hier auf der Website im Downloadthema zum Beweis des Alternativsatzes.  

Die inhomogene Version des Satzes von Stiemke dagegen bedeutet geometrisch, dass der Vektor b ∈ ℝ^m entweder gemäß (2”) im Bild des positiven Orthanten ℝⁿ₊ bei der durch A(x) = Ax vermittelten linearen Abbildung A : ℝⁿ → ℝ^m liegt,

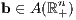
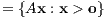
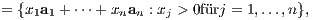
oder gemäß (1”) sich von diesem Bild derart trennen lässt, dass eine Hyperebene H_z,0 existiert mit

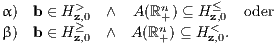
Im Fall (1”) sind die Mengen {b} und A(ℝⁿ₊) also sogenannte eigentlich trennbare Mengen. Die Menge A(ℝⁿ₊) ist die Menge aller Positivkombinationen (positiven Linearkombinationen) der Spalten a_j der Matrix A. Während im Fall (I) des Minkowski-Farkas-Lemmas der Vektor b ∈ ℝ^m nur im offenen Halbraum liegen kann, kann im entsprechenden Fall (1”) der inhomogenen Version des Satzes von Stiemke der Vektor b ∈ ℝ^m sowohl im offenen Halbraum (Fall 1”α) als auch im abgeschlossenen Halbraum (Fall 1”β) liegen. Eine ausführlichere Begründung für die geometrische Interpretation der Fälle 1“a) und 1“β) der inhomogenen Version des Satzes von Stiemke findet man im nachfolgend angegebenen Buch des Autors oder hier auf der Website im Downloadthema zum Beweis des Alternativsatzes. 

 

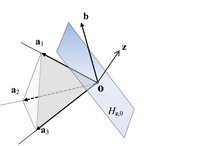
Abb. 2 Der Fall (I) im Minkowski-Farkas-Lemma bzw. der Fall (1”α) in der inhomogenen Version des Satzes von Stiemke, in dem b außerhalb des Kegels cone {a₁,a₂,a₃} liegt (m = n = 3)

Literatur

Rudolf Pleier (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage.