Dr. Dr. Rudolf Pleier

Das Einperiodenmodell als Spezialfall des Mehrperiodenmodells und in spezieller Darstellung

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015 / Juli 2018

Nachfolgend werden die beim Thema „Das Mehrperiodenmodell zur Beurteilung unsicherer Zahlungsströme bei vollkommenem Kapitalmarkt“ angegebenen Begriffe und Bezeichnungen verwendet. Die für das Mehrperiodenmodell (englisch: multi-period model) hergeleiteten Charakterisierungen der zentralen Be­griffe Vollständigkeit, Law of One Price und Arbitragefreiheit werden nun in der speziellen Schreibweise des Einperiodenmodells (englisch: one period model) formuliert. Im Mehrperiodenmodell (T ∈ ℕ) kann eine Matrizenschreibweise für die lineare Abbildung

                                   

(V_t(h)(ω) = S_t^δ(ω)^⊤h_t(ω),  R_t(h)(ω) = S_t(ω)^⊤h_t+1(ω), t ∈ I = {0,…,T}, ω ∈ Ω ={ω₁,...,ω_K}) durch 

                                   L(h) = L·h

mit der Matrix L gegeben werden:

mit

Eine ausführlichere Darstellung findet man im unten angegebenen Buch des Autors.
 

Im Spezialfall des Einperiodenmodells (T = 1) erhält man für die Abbildung L die Darstellung

                               

also

                              

mit der (1+K)×2N-Darstellungsmatrix

                              

Die zur linearen Abbildung L : ℝ^2N → ℝ^1+K eindeutig bestimmte adjungierte Abbildung L* : ℝ^1+K → ℝ^2N besitzt die Darstellungsmatrix

                                

 

Neben den Matrizen L und L^⊤ werden noch die Teilmatrizen

                             

und

                             

verwendet. Für die additive Zerlegung der linearen Abbildungen L und L* = L^T in deter­mi­nis­ti­schen und stochastischen Anteil erhält man im Einperiodenmodell die Matrix­darstellungen  

                             

mit

                           

Mit den Bildräumen und Kernen der linearen Abbildungen

                          D^T : ℝ^N ™→ ℝ^K  und  D : ℝ^K →™ ℝ^N

lassen sich die Vektorräume ℝ^N und ℝ^K als direkte Summen von orthogonalen Komplementen darstellen:

                          ℝ^N = ker D^T ⊕ D(ℝ^K),       (ker D^T)^⊥ = D(ℝ^K), 

                          ℝ^K = ker D ⊕ D^T(ℝ^N),       (ker D)^⊥ = D^T(ℝ^N).  

 

Das Einperiodenmodell ist nicht nur ein Spezialfall des Mehrperiodenmodells, sondern nimmt auch mit seiner in der Literatur gebräuchlichen speziellen Formulierung eine Sonderstellung ein. An die Stelle der Abbildungen L und L^T in den Räumen ℝ^2N und ℝ^1+K können wie in der Literatur üblich die Abbildungen D^T, S₀^T und D in den niedriger­dimensio­na­len Räumen ℝ^N und ℝ^K treten. Diese Darstellung wird ermöglicht durch die drei folgenden Ei­genschaften: 1) Die Handelsstrategien h = (h₀,h₁)^T sind deterministisch, also die Zustandsfunkti­onen h₀ und h₁ auf Ω konstant und somit als N-Tupel h₀, h₁ ∈ ℝ^N zu beschreiben. 2) Im Zahlungsprofil X = (X₀,X₁)^T ∈ 𝒲 ist die Zustandsfunktion X₀ : Ω → ℝ deterministisch, also konstant auf Ω, sodass das zugehörige K-Tupel (X_0,1,…,X_0,K)^T ∈ ℝ^K identische Komponen­ten X_0,1 = … = X_0,K = X₀ besitzt und als Skalar X₀ ∈ ℝ beschreibbar ist. Die Zustandsfunktion X₁ : Ω → ℝ ist stochastisch und durch das K-Tupel (X_1,1,…,X_1,K)^T ∈ ℝ^K darstellbar. 3) Da aufgrund der ersten Duplikationsgleichung der Wert der Nutzenfunktion für die Duplikationsstrategien h von X ∈ L(ℝ^2N) sich auch mittels R₀(h) =S₀^Th₁  berech­nen lässt, kann man in der additiven Zerlegung von L den deterministischen Bewer­tungsterm mit außer Acht lassen und statt L zunächst nur die deterministi­sche Abbildung S₀^T und die stochastische Abbildung mit L‘ = (‑S₀^T,D^T)^T und schließlich nur noch die Abbil­dungen S₀^T und D^T betrachten.        

 

1     Das Einperiodenmodell als Spezialfall des Mehrperiodenmodells

Ausgehend von den im Buch des Autors (bzw. im entsprechenden Thema dieser Website) für das Mehrperiodenmodell angegebenen Charakterisierungen der Vollständigkeit 

(VS)                   L(ℋ_N) = 𝒲

des Marktmodells ((S,δ),ℱ) (englisch: complete market model), der Gültigkeit des Law of One Price (Gesetz des eindeutig bestimmten Preises, Abk.: LOP) 

(LOP)              Für jedes X ∈ L(ℋ_N) gilt: V₀(h) = S₀^δTh₀  ist konstant ∀ h ∈  L^‑1({X})  

und der Arbitragefreiheit (englisch: No-Arbitrage Principle, Arbitrage-Free Condition)

(AF)                ∄ h ∈ ℋ_N mit V₀(h) = S₀^δTh₀ = 0  ∧  L(h) 0 (d. h. L(h) ≥ 0 und L(h) ≠ 0)

können diese in einfacher Weise als Charakterisierungen für den Spezialfall des Einperioden­mo­dells (T = 1) geschrieben werden: Dazu ersetzt man einfach die Begriffe ℋ_N, 𝒲, b = (S₀^δ)_0,Ω ∈ ℋ_N, 1_0,Ω ∈ 𝒲, ℰ = lin 1_0,Ω und L* durch ℝ^2N, ℝ^1+K, b = (S₀^δ,0)^T ∈ ℝ^2N, 1_0,Ω = (1,0)^T ∈ ℝ^1+K, ℰ =lin 1_0,Ω und L^T. Diese Charakterisierungen werden vorneweg in Tabelle 1 aufgelistet. Dabei werden noch die folgenden Unterräume von ℝ^2N bzw. ℝ^1+K und Orthanten von ℝ^1+K verwendet:

                      ℬ := [b] :=lin {b},                                          ℬ^⊥ = ker b^T = ker V₀,  

                     ℳ := L(ker V₀) = L‘(ℝ^N) ⊆ L(ℝ^2N),                ℳ^⊥ = L*^-1(ℬ) = ker L‘^T,

                     𝒱  := {v₀(h)1_0,Ω : h ∈ ℝ^2N},

                     ℰ := lin 1_0,Ω = lin {L(b)} = L(ℬ) ⊆ L(ℝ^2N),      ℰ^⊥ = {X ∈ ℝ^1+K : X₀ = 0},

                    = {X ∈ ℝ^1+K : X ≥ 0 , X ≠ 0},                   = {X ∈ ℝ^1+K : X > 0}.

Anschließend werden aber noch analoge Aussagen für das Einperiodenmodell mittels der in der Literatur übli­chen speziellen Darstellungsweise mit den linearen Abbildungen D, D^T und S₀^T der niedriger­dimen­sio­nalen Räume ℝ^N, ℝ^K und ℝ in Tabelle 2 angegeben. Diese kön­nen entweder aus den Aussagen des Mehrperioden­modells abgelei­tet werden oder extra im Ein­periodenmodell bewie­sen werden. Damit er­hält man sowohl die bekannten Aussagen, die schon in der ausführlichen Darstellung des Einpe­riodenmodells bei Kremer (2011), S. 3–71, zu finden sind, als auch wei­tere neue Aussagen.  

 

Tab. 1  Die im Mehrperiodenmodell (T ∈ ℕ) entwickelten Charakterisierungen der Duplizierbarkeit, der Vollstän­dig­keit, des Law of One Price und der Arbitrage­freiheit in der Formulierung für das Einperiodenmodell (T = 1)    

Duplizierbarkeit (DP)
Vollständigkeit (VS)
Law of One Price (LOP)
LOP nicht gültig
(VS) ∧ LOP
(VS) ∧ 2N = 1+K
(VS) ∧ LOP ungültig
Arbitragefreiheit (AF)
(VS) ∧ (AF)

 

2     Das Einperiodenmodell in der speziellen Darstellung in den niedrigerdimensionalen Räumen ℝ^N und ℝ^K     

2.1  Die Charakterisierungen der Vollständigkeit

Im Einperiodenmodell heißt ein Zah­lungsprofil

                        X = (X₀,X₁)^T = (X₀,X₁(ω₁),…, X₁(ω_K))^⊤ ∈ ℝ^1+K,

dupli­zierbar (erreich­bar, absicherbar; englisch: attainable, hedge­able, marke­table), wenn X das bei der Abbildung L sich ergebende Bild Lh einer Han­dels­­strategie h ∈ ℝ^2N ist. Die Überein­stim­mung der stochastischen Prozesse X und Lh soll dabei für beide Zeitpunkte t = 0, 1 und im Zeit­punkt t = 1 für alle Zustände ω_k ∈ Ω (k =1,...,K) gel­ten, somit P-si­cher erfüllt sein (P ist das W-Maß auf ). X ist also genau dann duplizierbar, wenn das gestaffelte inhomogene lineare Gleichungs­system

lösbar ist. Die Bestimmung einer Duplikationsstrategie h von X ∈ L(ℝ^2N) erfolgt also linear­algeb­raisch durch das Lösen eines linearen Gleichungssystems und nicht wahrschein­lich­keits­theore­tisch. Die tatsächlichen Eintrittswahrscheinlichkeiten P(ω) der Zustände ω ∈ Ω werden nicht be­nötigt. Da bei gültigem LOP jedes duplizierbare Zahlungsprofil X ∈ L(ℝ^2N) durch den für seine Dupli­kationsstrategien h ∈ L^‑1({X}) konstanten und deterministischen Wert π(X) = V₀(h) =S₀^δ⊤h₀ bewertet wird, ist diese Bewertung von X ebenfalls linearalgebraisch und nicht wahr­scheinlichkeitstheoretisch. Es handelt sich außerdem um einen relativen Bewertungsansatz, da hierzu eine spezielle Auswahl von Wertpapieren S ^j (j = 1,…,N) zugrunde gelegt ist und die Bewertung auf mittels Handels­strategien h dupli­zier­bare Zahlungspro­file X eingeschränkt ist.    

Die Vollständigkeit (VS) des Marktmodells bedeutet, dass jedes X = (X₀,X₁)^⊤ ∈ ℝ^1+K duplizierbar ist, also für beliebig vorgegebene X₀ ∈ ℝ und X₁ ∈ ℝ^K die beiden Gleichungen     

                      

lösbar sind. Da unter der mathematisch-technischen Voraussetzung  S₀^δ ≠ 0 die erste Glei­chung für beliebige X₀ ∈ ℝ, h₁ ∈ ℝ^N stets nach h₀ auflösbar ist, ist dies gleichbedeutend zur Lösbarkeit von D^Th₁ = X₁. In den niedrigerdimensionalen Räumen ℝ^N und ℝ^K des Einperiodenmodells wird die Vollständigkeit des Marktmodells also charakterisiert durch die Surjektivität der Abbildung D^T : h₁ ∈ ℝ^N ⟼ D^Th₁ ∈ ℝ^K:           

                        (VS) ⇔ Im D^T := D^T(ℝ^N) = ℝ^K.

Wegen der Darstellung von ℝ^K als direkte Summe

                       ℝ^K = Im D^T ⊕ ker D,        (Im D^T)^⊥ = ker D,    

der orthogonalen Komplemente Im D^T und ker D ist die Vollständigkeit (VS) auch äquivalent zu ker D = O = {0}, also zur Injektivität der linearen Abbildung D : X₁ ∈ ℝ^K ⟼ DX₁ ∈ ℝ^N. Es gilt also auch           

                      (VS) ⇔ ker D = O.

 

2.2  Die Charakterisierungen des Law of One Price

Mit der Handelsstrategie

b := (b₀,0)^⊤ = (S₀^δ,0)^⊤ ∈ ℋ_N bzw. ∈ ℝ^2N

und dem davon aufgespannten eindimensionalen Unterraum ℬ := lin {b} von ℋ_N bzw. ℝ^2N erhält man die deterministische Linearform  

deren Kern

       

und dessen L-Bild   

als die Menge der Kapitalmarktgeschäfte (Begründung der Bezeichnung in der pdf-Datei). Im Einperiodenmodell gibt es für die Zahlungsströme Z ∈ ℳ die folgende Charakterisierung:

Aufgrund der Darstellung von ℝ^1+K als direkte Summe

 ℝ^1+K = Im L‘ ⊕ ker L‘^⊤,              (Im L‘)^⊥ = ker L‘^⊤,  

der orthogonalen Komplemente Im L‘ und ker L‘^⊤ erhält man das orthogonale Komplement ℳ^⊥ von ℳ durch  

Im Einperiodenmodell ist also im Raum ℝ^1+K die Menge ℳ der Kapitalmarktgeschäfte gegeben durch das Bild der Abbildung L‘,

und das orthogonale Komplement ℳ^⊥ von ℳ durch den Kern der Abbildung L‘^⊤,

 

Im Mehrperiodenmodell ist das LOP äquivalent zur Inzidenz

b ∈ L*(𝒲),

also zur Existenz eines Ψ ∈ 𝒲 mit L*(Ψ) = b. Speziell im Einperiodenmodell bedeutet dies die Existenz eines Ψ = (Ψ₀,Ψ₁)^⊤ ∈ ℝ^1+K mit

also wegen S₀^δ ≠ 0 die Existenz eines Ψ = (Ψ₀,Ψ₁)^⊤ ∈ ℝ^1+K mit

 Wie allgemein im Mehrperiodenmodell, so ist also auch hier die Existenz eines Ψ ∈ ℝ^1+K mit L^⊤Ψ = b äquivalent zur Existenz eines Ψ ∈ ℳ^⊥ mit Ψ₀ = 1. Damit erhält man folgende wei­tere Charakterisierungen für das LOP:

Das LOP bedeutet also, dass im Kern von L‘^⊤ = (-S₀,D) ein nichttrivialer Vektor Ψ mit der ersten Komponente Ψ₀ = 1 existiert, also S₀ linear abhängig von den Spalten von D ist bzw. dass die erste Spalte ‑S₀ von L‘^⊤ auch schon im Spaltenraum von D liegt. Diese Charakterisierung des LOP wird auch noch innerhalb der Räume ℝ^N und ℝ^K in der zugehörigen pdf-Datei bewiesen.    

In einem Einperiodenmodell mit gültigem LOP ist die Lösung Ψ₁ von DΨ₁ = S₀,

Ψ₁ ∈ Ψ₁‘ + ker D mit einer speziellen Lösung Ψ₁‘ von DΨ₁‘ = S₀,

genau dann eindeutig bestimmt, wenn ker D = O, also das Marktmodell auch noch vollständig ist.

Aufgrund der Charakterisierung des LOP durch die Bedingung S₀ ∈ Im D und wegen der Dar­stel­lung von ℝ^N als direkte Summe

ℝ^N = ker D^T ⊕ D(ℝ^K),       (ker D^T)^⊥ = D(ℝ^K), 

der orthogonalen Komplemente Im D und ker D^T ist das LOP auch äquivalent zu S₀ ⊥ ker D^T bzw. zu ker D^T ⊆ [S₀]^⊥ = ker S₀^T und damit zu ker L‘ = ker S₀^⊤ ∩ ker D^T = ker D^T:    

Für die Charakterisierung des LOP durch ker D^T ⊆ ker S₀^T wird in der pdf-Datei auch noch eine Begründung in­nerhalb der Räume ℝ^N und ℝ^K angegeben. Eine graphische Darstellung die­ser geometrischen Situation wird in den Ab­bildungen 1 und 2 für die Zahlungsprofile X ∈ ℝ^1+K und in Abbildung 3 für die Zahlungsprofile X₁ ∈ ℝ^K gegeben.

 

Weiter ist im Mehrperiodenmodell das LOP äquivalent zur Gültigkeit der Preisgleichungen für die mittels L duplizierbaren (erreichbaren) Zahlungsprofile X = L(h) ∈ L(ℋ_N) mit einem Prozess Ψ ∈ 𝒲 (Ψ₀ = 1):

Ein derartiger Prozess Ψ ∈ 𝒲 liefert für jedes Zahlungsprofil X ∈ L(ℋ_N) mit dem Skalarprodukt

von Ψ und X den Preis von X und wird daher als Bewertungsprozess für die duplizierbaren Zahlungsprofile X = L(h) ∈ L(ℋ_N) bezeichnet.

Im Einperiodenmodell bedeutet (PGΨ) die Existenz eines Bewertungsprozesses Ψ = (Ψ₀,Ψ₁)^⊤ ∈ ℝ^1+K, Ψ₀ = 1, d. h. die Gültigkeit der Preisgleichung für die duplizierbaren Zahlungsprofile X = Lh  ∈ L(ℝ^2N): 

also die Existenz eines sog.  Bewertungsvektors Ψ₁ ∈ ℝ^K für die duplizierbaren Zahlungsprofile X₁ = D^Th₁ ∈ D^T(ℝ^N):

Für die Äquivalenz von LOP und (PGΨ1) wird in der zu diesem Thema gehörigen pdf-Datei auch noch eine Begründung innerhalb der Räume ℝ^N und ℝ^K angegeben. Weiter wird in der pdf-Datei begründet, dass das LOP für die X = (X₀,X₁)^T ∈ L(ℝ^2N) äquivalent ist zur Be­dingung

und zu dem folgenden Law of One Price für die X₁ ∈ D^T(ℝ^N):   

Der Preis π₁(X₁) des zum Zeitpunkt t = 1 auftretenden Zahlungsprofils X₁ = D^Th₁ ∈ D^T(ℝ^N) kann dann in Übereinstimmung mit dem Preis

des Zahlungsprofils 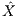 = (0,X₁)^T ∈ L(ℝ^2N) (X₀ = 0) durch S₀^⊤h₁ definiert werden:

Nach (PGΨ1) erhält man bei bekanntem Be­wertungsvektor Ψ₁ den Preis π(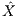) von 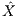 = (0,X₁)^T ∈ L(ℝ^2N) und den Preis π₁(X₁) von X₁ = D^Th₁ ∈ D^T(ℝ^N) auch als das Skalarpro­dukt von Ψ₁ und X₁, ohne eine Duplikationsstrategie be­rechnen zu müssen:

Demnach kann das Gleichungssystem (PGΨ1) als das System der Preisgleichungen für die mittels L duplizierbaren Zahlungsprofile 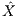= (0,X₁)^⊤ = Lh  ∈ L(ℝ^2N) ⊆ ℝ^1+K bzw. für die stochastischen Anteile 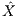= (0,X₁)^⊤  der mittels L duplizierbaren Zahlungsprofile X = (X₀,X₁)^⊤ = Lh  ∈ L(ℝ^2N) ⊆ ℝ^1+K bzw. für die mittels D^⊤ duplizierbaren Zahlungsprofile X₁ ∈ D^⊤(ℝ^N) ⊆ ℝ^K angesehen werden kann. Bei Kremer (2011) wird im Einperiodenmodell nur der Spezialfall der Zahlungsprofile X = (X₀,X₁)^⊤ ∈ ℝ^1+K mit X₀ = 0, X = ( 0,X₁)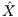^⊤ = = Lh  ∈ L(ℝ^2N) bzw. der zum Zeitpunkt t = 1 gehörigen Zahlungsprofile X₁ mit dem Preis π₁(X₁) = π(X) = S₀^⊤h₁ behandelt. 

 

Zur Formulierung weiterer Charakterisierungen der Begriffe Law of One Price und Arbitragefreiheit in den niedrigerdimensionalen Räumen ℝ^N, ℝ^K und ℝ werden noch fol­gende Unterräume von ℝ^N bzw. ℝ^K und Orthanten von ℝ^K benötigt:

Es wird dabei die mathematisch-technische Voraussetzung U₁ = D^TS₀ ≠ 0 verwendet. Die bei den nachfolgenden Bedingungen auftretenden stochastischen Vektoren Ψ₁, Φ₁ ∈ ℳ₁^⊥ \ ker D ⊆ ℝ^K werden als Bewertungsvektor bzw. Diskontvektor (Zustands(preis)vektor) für die duplizierbaren Zahlungs­profile X₁ = D^Th₁ ∈ D^T(ℝ^N) bezeichnet. Die Beweise der Aussagen sind vollständig in der pdf-Datei angegeben.          

Bei den nachfolgenden Charakte­ri­sie­run­gen des Law of One Price und der Arbitragefreiheit werden nicht nur lineare Gleichungen für die Portfoliovektoren h₁ ∈ ℝ^N bzw. h₁ ∈ ker S₀^T, sondern auch Struktur und Lage­beziehungen für bestimmte Unterräume von ℝ^N und ℝ^K angegeben. Der Vorteil der neuen Charakterisierungen mittels der Vek­torunterräume besteht darin, dass sie bei­spielsweise durch die nachfolgende Abbildung 3 geometrisch visualisiert werden können. Ande­rerseits liefert eine geometrische Veranschaulichung auch eine Quelle für Vermutungen über weitere neue Ergebnisse. Der Vektorraum ℝ^K der stochastischen Zahlungsprofile X₁ lässt sich dar­stellen als di­rekte Summe der Unterräume D^T(ℝ^N) und ker D und als direkte Summe von ℳ₁ und ℳ₁^⊥. Dabei liegt stets ℳ₁ in D^T(ℝ^N)  und ker D in ℳ₁^⊥. In der Abbildung 4b ist dargestellt, dass bei ungülti­gem LOP sowohl der Unterraum ℳ₁ der NE-Zahlungsprofile (Nulleinsatz-Zahlungsprofile; Begründung der Bezeichnung in der pdf-Datei) mit dem Unterraum D^T(ℝ^N) der dupli­zierbaren Zahlungsprofile X₁ als auch der Unterraum ℳ₁^⊥ mit dem Unterraum ker D zu­sammen­fällt. In der Abbildung 4a sieht man dagegen, dass mit der Einstellung des LOP im Marktmodell der Unterraum ℳ₁ um eine Dimension kleiner ausfällt als der Unterraum D^T(ℝ^N) und der Unter­raum ℳ₁^⊥ um eine Dimension größer wird als ker D. Im nichtleeren Be­reich ℳ₁^⊥  \ ker D liegt dann ein Bewertungsvektor Ψ₁, mit dem der Preis π₁(X₁) eines duplizier­baren Zahlungs­profils X₁ ∈ D^T(ℝ^N)  als Skalarprodukt Ψ₁^TX₁ und somit unabhängig von einer Duplika­tionsstrategie berechnet werden kann: Für diesen Vektor Ψ₁ ∈ ℝ^K gilt nämlich o. E. DΨ₁ = S₀, sodass für ein festes Zahlungsprofil X₁ ∈ D^T(ℝ^N) alle Duplikations­strategien h₁ von X₁ durch die deterministische lineare Nutzenfunktion h₁ ↦ S₀^⊤h₁ mit dem gleichen Wert S₀^⊤h₁ = Ψ₁^TD^Th₁ = Ψ₁^TX₁ bewer­tet werden. Da dieser Wert mit dem Preis π(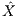) von 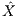 = (0,X₁)^T ∈ L(ℝ^2N) überein­stimmt, wird er auch als Preis π₁(X₁) von X₁ bezeichnet. Demzufolge ist die auf ℝ^K defi­nierte Linearform π₁(X₁) = Ψ₁^TX₁ eine lineare Nutzenfunktion, die auf D^T(ℝ^N) den Preis von X₁ liefert. 

 

Tab. 2  Die Charakterisierungen der Duplizierbarkeit, der Vollstän­dig­keit, des Law of One Price und der Arbitrage­freiheit in der speziellen Formulierung für das Einperiodenmodell mit den Abbildungen D, D^T, S₀^T der niedrigerdimensionalen Räume ℝ^1+K und ℝ^N   

Duplizierbarkeit (DP)
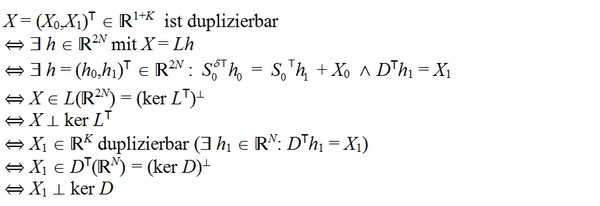Vollständigkeit (VS)
Law of One Price (LOP)
LOP nicht gültig
(VS) ∧ LOP
(VS) ∧ 2N = 1+K
(VS) ∧ N = K
(VS) ∧ LOP ungültig
Arbitragefreiheit (AF)
(VS) ∧ (AF)

 

 

a) LOP gültig:

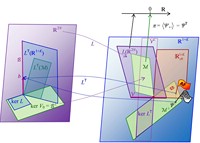
b) LOP ungültig:

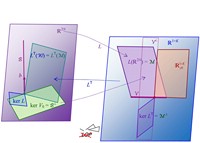
Abb. 1 Die verschiedenen Unterräume von ℝ^2N und ℝ^1+K und die linearen Abbildungen L und L^⊤:
a) bei gültigem LOP mit Bewertungsprozess Ψ bzw. bei vorliegender Arbitragefreiheit (AF) mit Zustandspreisprozess Φ;
b) bei ungültigem LOP   

 

a) VS und AF gültig:

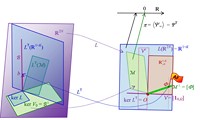
b) VS und LOP gültig:

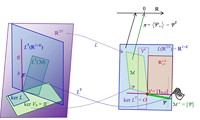
c) VS gültig und LOP ungültig:

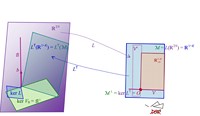
Abb. 2 Die verschiedenen Unterräume von ℝ^2N und ℝ^1+K und die linearen Abbildungen L und L^⊤ bei vollständigem Marktmodell und 
a) bei vorliegender Arbitragefreiheit (AF) mit Zustands­preis­prozess Φ,
b) bei gültigem LOP mit Bewertungsprozess Ψ, 
c) bei ungültigem LOP   

 

 

a) LOP gültig:

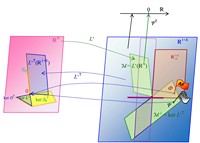
b) LOP ungültig:

 

 

 

 

 

 

 

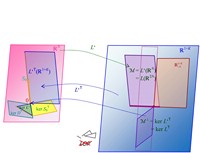
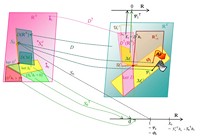
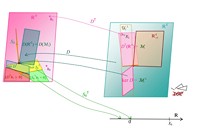
Abb. 3 Die verschiedenen Unterräume von ℝ^N und ℝ^1+K und die linearen Abbildungen L' und L'^⊤:
a) bei gültigem LOP mit Bewertungsprozess Ψ bzw. bei vorliegender Arbitragefreiheit (AF) mit Zustandspreisprozess Φ;
b) bei ungültigem LOP   

 

a) LOP gültig:

b) LOP ungültig:

 

 

 

 

 

 

 

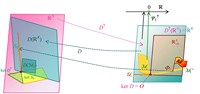
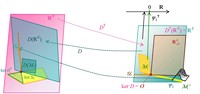
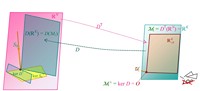
Abb. 4  Die verschiedenen Unterräume und Urbildmengen in ℝ^N und ℝ^K und die linearen Abbildungen S₀^T, D^T, S₀ und D:
a) bei gültigem LOP mit Bewertungsvektor Ψ₁ bzw. bei vorliegender Arbitragefreiheit (AF) mit Zustandspreisvektor Φ₁;
b) bei ungültigem LOP

 

a) VS und AF gültig:

b) VS und LOP gültig:

c) VS gültig und LOP ungültig:

Abb. 5  Die verschiedenen Unterräume und Urbildmengen in ℝ^N und ℝ^K und die linearen Abbildungen D^T und D bei vollständigem Marktmodell und 
a) bei vorliegender Arbitragefreiheit (AF) mit Zustands­preis­vektor Φ₁,
b) bei gültigem LOP mit Bewertungsvektor Ψ₁, 
c) bei ungültigem LOP   

 

2.3  Die Charakterisierungen der Arbitragefreiheit

2.3.1 Der Fundamentalsatz der Preistheorie 

 

Im (zeitdiskreten) Mehrperiodenmodell besagt der Fundamentalsatz der Preistheorie, dass die Arbitragefreiheit

des Marktmodells äquivalent ist zur Existenz eines stochastischen Prozesses

eines sogenannten Zustands(preis)prozesses des Marktmodells. Der Beweis ergibt sich unmittelbar aus dem Alternativsatz über die Disjunktheit eines linearen Unterraums ℳ von zum schwach positiven Orthanten (siehe entsprechendes Thema auf dieser Website)

der dem Alternativsatz von Stiemke über die Lösbarkeit von homogenen linearen Ungleichungssystemen entspricht.

Im Einperiodenmodell ist die Arbitragefreiheit (AF) folgendermaßen definiert und charakte­ri­siert:

Geometrisch bedeutet die Arbitragefreiheit (AF), dass in ℝ^N bestimmte verallgemeinerte polyedrische Kegel leer sind. Beispielsweise ist für (AF0) {S₀^Th₁ < 0 , D^Th₁ ≥ 0} = ∅ und für (AF1) {S₀^Th₁ ≤ 0 , D^Th₁  0} = ∅. Weiter kann die Arbitragefreiheit (AF) geometrisch durch die Lage der S₀^T-Bilder von {D^Th₁ ≥ 0}, {D^Th₁ 0} und {D^Th₁ = 0} = ker D^T zur negativen bzw. nichtpositiven Halbachse in ℝ und durch die Lage der D^T-Bilder von {S₀^Th₁ < 0}, {S₀^Th₁ ≤ 0} und {S₀^Th₁ = 0} = ker S₀^T bezüglich des nichtnegativen bzw. schwach positiven Orthanten und des Nullpunkts O in ℝ^K beschrieben werden:  

Die Arbitragefreiheit (AF) bedeutet, dass es in ℝ^1+K kein Kapitalmarktgeschäft Z = (Z₀,Z₁)^T ∈ ℳ = L’(ℝ^N) gibt, das schwach positiv ist (Z  0). Sie kann aber in ℝ^K nicht allein durch die spezielle Arbit­rage­freiheit (AF1.0) charakte­ri­siert werden, nach der es kein schwach positives NE-Zahlungsprofil Z₁ ∈ ℳ₁ = D^T([S₀]^⊥) = D^T({S₀^Th₁ = 0}) gibt. Viel­mehr muss im Allgemeinen in ℝ^K auch noch die spezielle Arbitragefreiheit (AF0) erfüllt sein, nach der auch kein nichtnega­ti­ves duplizier­bares Zah­lungsprofil X₁ = D^Th₁ ∈ D^T(ℝ^N) existiert, für dessen Duplika­tions­strate­gie h₁ der Wert S₀^Th₁ ne­gativ ist. Im nachfolgenden Abschnitt 2.3.2 wird aber eine Zusatzvoraussetzung an das Marktmodell angegeben, unter der die spezielle Arbitragefreiheit (AF1.0) äquivalent ist zur allgemeinen Arbitrage­freiheit (AF) (also inklusive (AF0)). 

 

Im Einperiodenmodell ist nach dem Fundamentalsatz der Preistheorie die Arbitra­ge­freiheit (AF) äquivalent zur Exis­tenz eines Zustandspreisprozesses, d. h. eines positiven Pro­zesses Φ ∈ ℳ^⊥ = ker L‘^T, also eines Prozesses Φ = (Φ₀,Φ₁)^T ∈ ℝ^1+K mit

                        L‘^TΦ  = 0  ∧ Φ > 0    

bzw.

                        DΦ₁ = S₀Φ₀  ∧ Φ₁ > 0, Φ₀ > 0.       

Die Arbitragefreiheit (AF) bedeutet also die Existenz eines positiven Vektors Φ₁ ∈ ℝ^K mit DΦ₁ = λS₀ und λ = λ(Φ₁) = Φ₀ > 0. Das D-Bild DΦ₁ von Φ₁ ist hier ein positives Vielfaches von S₀. Ohne Einschränkung (ggf. durch Übergang von Φ zu Φ/Φ₀) kann Φ als ein mit Φ₀ = 1 nor­mier­ter Zustandspreisprozess (Diskontierungsprozess) gewählt werden. Die Arbitrage­freiheit ist also auch äquivalent zur Existenz eines Diskontierungsprozesses Φ ∈ ℝ^1+K, d. h.    

                        Φ = (1,Φ₁)^T > 0  ,  L‘^TΦ  = 0,  

bzw. zur Existenz eines sogenannten Diskontvektors (Zustands(preis)vektors) Φ₁ ∈ ℝ^K mit den Eigenschaften     

                        Φ₁ > 0  ,  DΦ₁ = S₀.       

In diesem Fall ist also der zum Zeitpunkt t = 0 gehörige deterministische Preisvektor S₀, der in der Nutzenfunktion S₀^T den Bewertungsvektor für die Portfoliovektoren h₁ darstellt, eine Posi­tivkombination (positive Linearkombination) der Spalten von D.  

Da der normierte Zustandspreisprozess Φ ein positiver Bewertungsprozess Ψ für die Zahlungs­profile X ∈ L(ℝ^2N), 

                        Ψ ∈ ℳ^⊥  mit Ψ₀ = 1 und Ψ > 0,

bzw. der Zustandspreisvektor Φ₁ ein positiver Bewertungsvektor Ψ₁ für die X₁ ∈ D^T(ℝ^N),  

                        Ψ₁ ∈ ℝ^K mit DΨ₁ = S₀ und Ψ₁ > 0, 

ist, stellt ein arbitragefreies Einperiodenmodell also ein Marktmodell dar, in dem das LOP gilt und zusätzlich der Bewer­tungs­prozess Φ bzw. der Be­wertungs­vektor Φ₁ positiv gewählt werden kann. Damit erhält man aus den oben hergeleiteten Charakterisierungen des LOP mittels des Bewer­tungsvektors Ψ₁ auch Charakterisierungen der Arbitragefreiheit, wenn man noch die Be­dingung Ψ₁ = Φ₁ > 0 hinzu­nimmt. Diese Charakterisierungen sind in Tabelle 2 aufge­führt. Bei­spielsweise ist ein arbitragefreies Einperiodenmodell dadurch charakterisiert, dass es einen positiven Vektor Φ₁ ∈ ℝ^K gibt, mit dem die Preisgleichungen für alle duplizierbaren Zahlungsprofile X₁ ∈ D^T(ℝ^N) gelten:

(PGΦ1)           ∃ Φ₁ ∈ ℝ^K  mit Φ₁ > 0  und  Φ₁D^Th₁ = S₀^Th₁  ∀ h₁ ∈ ℝ^N.       

Weiter wird die Arbitragefreiheit im Einperiodenmodell dadurch charakterisiert, dass es einen posi­tiven Vektor Φ₁ ∈ ℝ^K gibt, mit dem ℳ₁^⊥ die direkte Summe von ker D und dem eindimen­sio­na­len Unterraum lin Φ₁ ist:

                        ℳ₁^⊥ = ker D ⊕ lin Φ₁.          

Für die duplizierbaren Zahlungsprofile X₁ ∈ D^T(ℝ^N) = 𝒰₁ ⊕ ℳ₁ hat man die Darstellung

                        X₁ = λU₁ + Z₁        

mit eindeutig bestimmten Beurteilungsparameter λ ∈ ℝ, NE-Zahlungsprofil Z₁ ∈ ℳ₁ und dem Preis

                       π₁(X₁) = Φ₁^TX₁ = λΦ₁^TU₁ + Φ₁^TZ₁ = λπ₁(U₁).   

Das gleichzeitige Auftreten der Arbitragefreiheit (AF) und Vollständigkeit (VS) ist äquiva­lent dazu, dass S₀ genau ein D‑Urbild Φ₁ besitzt und dieses Urbild Φ₁ positiv ist:   

                          

In diesem Fall (AF) ∧ (VS) ist dann

                                

 

2.3.2 Eine hinreichende Bedingung für die Äquivalenz der allgemeinen Arbi­trage­freiheit (AF) zur speziellen Arbitragefreiheit (AF1.0)     

Es wird nun ein Marktmodell betrachtet, für welches die Bedingung (AF1.0) der speziellen Arbit­ragefreiheit erfüllt ist. Es soll unter­sucht werden, ob unter einer Zusatzvoraussetzung dann auch die zweite Bedingung (AF0) für die allgemeine Arbitragefreiheit (AF) = (AF0) ∧ (AF1.0) gesi­chert werden kann.

Die spezielle Arbitragefreiheit

(AF1.0)    

ist nach dem Alternativsatz über die Disjunktheit eines linearen Unter­raums ℳ₁ von ℝ^K zum schwach positiven Orthanten   äqui­va­lent zur Existenz eines positi­ven Vektors Φ₁ ∈ ℳ₁^⊥ = D^-1([S₀]) (zur Darstellung von ℳ₁^⊥ als Urbild­menge siehe Beweisteil 8a), also eines positiven Urbildes in der D-Urbildmenge von [S₀]:

 

Für beliebige Portfoliovektoren h₁ ∈ ℝ^N bzw. für beliebige duplizierbare Zahlungsprofile X₁ = D^Th₁ ∈ D^T(ℝ^N) gilt dann die Gleichung 

(PGΦ₁λ)         λS₀^Th₁ = Φ₁^TD^Th₁.        

Über das Vorzeichen des zu Φ₁ gehörigen Parameters λ(Φ₁) wird hierbei nichts ausgesagt. Es kann gezeigt werden, dass ein positiver Parameter λ(Φ₁) die Existenz eines Zustandspreisvektors Φ₁ und damit die allgemeine Arbitragefreiheit (AF) sichert. Der Beweis hierfür und für die nachfolgenden Aussagen befindet sich in der zugehörigen pdf-Datei. Weiter kann gezeigt werden, dass unter der mathematisch-technischen Zusatzvoraussetzung

(SPDZ)           ∃ g₁ ∈ ℝ^N bzw. Z₁ = D^Tg₁ ∈ D^T(ℝ^N) mit  

umgekehrt die Bedingung λ = λ(Φ₁) > 0 für jeden positiven Vektor Φ₁ ∈ ℳ₁^⊥ = D^-1([S₀]) auch notwendig für die Gültigkeit von (AF) bzw. (AF0) ist. Die Voraussetzung (SPDZ) besagt, dass in ℝ^N die Menge nichtleer ist bzw. in ℝ^K die Menge nichtleer ist, also ein schwach positives D^T-Bild existiert. Unter den Voraussetzungen (SPDZ) und (AF1.0) gilt also für alle : 

       

Anstelle der Voraussetzung (SPDZ) wird nun die stärkere Zusatzvoraussetzung (GI) an das Markt­mo­dell gestellt, dass auf dem Kapitalmarkt ℳ = L‘(ℝ^N) ⊆ ℝ^1+K des Marktmodells eine gewinn­bringende In­vestition Y = (Y₀,Y₁)^T = L‘k₁ existiert. Bei dieser Investition Y ∈ ℝ^1+K soll zum Zeitpunkt t = 0 eine Auszahlung Y₀ < 0, zum Zeitpunkt t = 1 in jedem Zustand ω_k ∈ Ω eine nichtnegative Zah­lung Y₁(ω_k) und in mindes­tens einem Zustand ω_k‘ eine positive Zahlung Y₁(ω_k‘) erfolgen:    

(GI)                    

Die Voraussetzung (GI) bedeutet, dass in ℝ^N die Menge

nichtleer, in ℝ^K die Menge

  

nichtleer bzw. in ℝ^1+K die Menge

nichtleer ist. Mit (GI) ist also auch die Voraussetzung (SPDZ) erfüllt. Unter der stärkeren Voraussetzung (GI) kann aber aus der speziellen Arbitrage­frei­heit (AF1.0) (d. h. beim Fehlen der speziellen Arbitrage­gelegen­heiten h₁ mit ) auch noch λ(Φ₁) > 0  geschlossen werden. Damit ist dann (AF1.0) gleich­be­deu­tend zur allge­mei­nen Arbitragefreiheit (AF) (inklu­sive (AF0):      

 

2.3.3 Formales Wahrscheinlichkeitsmaß, Preismaß, Martingalmaß und risikoneutrales Wahr­schein­lich­keitsmaß       

In der pdf-Datei zu dem vorliegenden Thema werden noch einige in der Literatur vielzitierte Begriffe im Einperioden­modell erläutert. Es sind dies die in der Überschrift aufgeführten Bezeichnungen und außerdem die Begriffe Arrow-Debreu-Preis, Er­eig­nis­preis, Zustandspreis, Zustands­preis­vektor, stochastischer Diskon­tie­rungs­fak­tor, de­termi­nis­ti­scher Diskon­tie­rungs­faktor und risikoneutrale Bewertung. Mittels der Duplizierbarkeit bestimmter Arrow-Debreu-Zahlungs­profile (1_C, C ⊆ Ω) werden dabei auch die meist weniger beachteten impliziten Prämissen dargestellt, unter denen die Begriffe erst einen Sinn haben. Bei der Behandlung des Martingalmaßes tritt an die Stelle der beim Mehrperiodenmodell verwendeten bedingten Erwartung  hier beim Einperiodenmodell nur der Erwartungswert. Im Einperiodenmodell sind die impliziten Prämissen für die Existenz des auf Ꮘ(Ω) definierten formalen W-Maßes Q₁ die Arbitragefreiheit (AF), für das Martingalmaß Q₁, das risikoneutrale bzw. risikolose Wahrscheinlichkeitsmaß Q₁ und die risikoneutrale Bewertung die Arbitragefreiheit (AF) und Voraussetzung (DPD^T1_Ω+). Die Voraussetzung (DPD^T1_Ω+), also die D^T-Duplizierbarkeit von 1_Ω = (1,...,1)^T ∈ ℝ^K zusammen mit der Positivität des Startkapitaleinsatzes einer Duplikationsstrategie von 1_Ω, entspricht dabei auch der Voraussetzung (FH) der Existenz einer festverzins­li­chen Handelsstrategie. Die impliziten Prämissen für das Preismaß Q₁ sind die Arbitragefreiheit (AF) und die Vollständigkeit (VS).

 

Literatur

[1]   Jürgen Kremer (2011), Portfoliotheorie, Risikomanagement und die Bewertung von Derivaten, Springer, Berlin Heidelberg.

[2]   Rudolf Pleier (2023), Diskrete stochastische Finanzmathematik, Tredition, Ahrensburg.