Ein streng monotoner Effektivzinssatz
⇒ Das Thema als PDF zum Download
Rudolf Pleier
Juni 2015
Für die in der Praxis verbreitete Ansicht, dass bei einer Finanzierung höhere Kreditgebühren bzw. höhere Rückzahlungen einen höheren Effektivzinsfaktor und umgekehrt Tilgungszuschüsse einen niedrigeren Effektivzinsfaktor bewirken, kann zunächst für reguläre Finanzierungen und dann noch für sog. NU-Finanzierungen eine mathematische Begründung gegeben werden. Dabei ist eine reguläre Finanzierung definitionsgemäß eine Finanzierung X = (X0,X1,…,Xn)T \(\in \mathbb{R}^{n+1} \) (X0 > 0) mit genau einem Vorzeichenwechsel in der Zahlungsfolge (Xj)j=0,…,n: Es gibt einen Index m ∈ {1,…,n} mit
X0 > 0, Xj ≥ 0 für j = 1,…,m‑1, Xm < 0, Xj ≤ 0 für j = m+1,…,n.
Eine NU-Finanzierung besitzt für ihre Barwertfunktion Bn(q) = Bn(X,q) genau eine positive Nullstelle qX, die außerdem noch eine Vorzeichenwechselstelle ist. Aufgrund des Grenzwertverhaltens der Barwertfunktion an den Grenzen des Intervalls ]0,∞[ besitzt die Barwertfunktion die Vorzeichenverteilung
Bn(X,q) < 0 für q ∈ ]0,qX[ und Bn(X,q) > 0 für q ∈ ]qX,∞[.
Bei der (strengen) Monotonie der Effektivzinsfaktor-Funktion (Interner Zinsfaktor-Funktion) qint(X) werden nur Argumente (unabhängige Variable) X, Y \(\in \mathbb{R}^{n+1} \) betrachtet, die mittels der natürlichen Halbordnung ≤ (bzw. der strengen Halbordnung \(\underset{\cdot}{<}\) = ≤ ∩ ≠) verglichen werden können.
Satz 1 Die streng monotone Abhängigkeit des Effektivzinssatzes einer regulären Finanzierung von Gebühren bzw. von Tilgungszuschüssen
1) Erhält man bei einer vorgegebenen regulären Finanzierung Y \(\in \mathbb{R}^{n+1} \) (Y0 > 0) durch die Vereinbarung von zu allen Zeitpunkten j = 0,…,n möglichen zusätzlichen Gebühren Gj ≥ 0 wieder eine reguläre Finanzierung
X = Y + D, D = ‑ G \(\underset{\cdot}{<}\) O,
so erhöht sich der nominelle Kreditzinsfaktor (Nominalzinsfaktor, interne Zinsfaktor) qY = qint(Y) des nominellen Zahlungsstroms Y auf den größeren Effektivzinsfaktor qX = qint(X) des effektiven Zahlungsstroms X:
qX > qY.
2) Werden dagegen zur regulären Finanzierung Y noch zusätzlich Tilgungszuschüsse Bj ≥ 0 vereinbart und ist auch der resultierende Zahlungsstrom
X = Y + D, D = + B \(\underset{\cdot}{>}\) O,
noch eine reguläre Finanzierung, so erniedrigt sich der Kreditzinsfaktor qY = qint(Y) von Y auf den kleineren Effektivzinsfaktor qX = qint(X) von X:
qX < qY.
Die gleichzeitige Hinzunahme von Gebühren und Zuschüssen ist hier nicht zugelassen.
3) Insgesamt erhält man aus 1) und 2) für direkt vergleichbare reguläre Finanzierungen X, Y \(\in \mathbb{R}^{n+1} \) (X \(\neq\) Y) und ihre eindeutig bestimmten positiven internen Zinsfaktoren qX = qint(X) und qY = qint(Y) die Aussagen:
i) X \(\underset{\cdot}{<}\) Y ⇔ qX > qY;
ii) X \(\underset{\cdot}{>}\) Y ⇔ qX < qY.
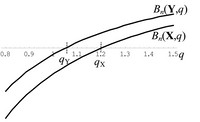
Abb. 1 Die Graphen der Barwertfunktionen Bn(X,q) und Bn(Y,q) der direkt vergleichbaren regulären Finanzierungen X und Y mit D = X - Y \(\underset{\cdot}{<}\) O und den internen Zinsfaktoren qX = qint(X) > qY = qint(Y)
Ein analoger Satz kann auch für direkt vergleichbare reguläre Investitionen (Anlagen, X0 < 0) mit Gebühren oder Sparzuschüssen (Boni) formuliert werden. Insgesamt ist dann sowohl für reguläre Finanzierungen als auch für reguläre Investitionen die Interner Zinsfaktor-Funktion streng monoton. Sie ist für reguläre Finanzierungen streng monoton fallend und für reguläre Investitionen streng monoton steigend.
Für diesen Satz werden in der PDF-Datei zwei Beweise angegeben. Ein erster kurzer und einfacher Beweis verwendet die Vorzeichenverteilung der Barwertfunktion einer regulären Finanzierung auf der positiven Halbachse ]0,∞[. Mit diesem ersten Beweisweg lässt sich der Satz auch verallgemeinern auf NU-Finanzierungen Z (Z0 > 0) bzw. NU-Investitionen Z (Z0 < 0). Für eine NU-Finanzierung Z hat die Barwertfunktion Bn(q) := Bn(Z,q) genau die im Beweis beschriebene Vorzeichenverteilung auf der positiven Halbachse: Bn(q) besitzt also genau eine positive Nullstelle. Diese ist noch eine Vorzeichenwechselstelle bzw. eine Nullstelle von ungerader Vielfachheit (Ordnung). Durch Beispiele kann gezeigt werden, dass die Aussage des Satzes für einen Zahlungsstrom, der nicht eine NU-Finanzierung oder eine NU-Investition ist, im Allgemeinen nicht gültig ist.
Ein zweiter aufwendigerer Beweis verwendet den Satz über implizite Funktionen, um die Existenz und strenge Monotonie der lokalen Interner Zinsfaktor-Funktion nachzuweisen. Weiter verwendet er, dass die Menge \(\Phi\) der regulären Finanzierungen wegzusammenhängend ist und je zwei direkt vergleichbare Punkte X und Y dieser Menge \(\Phi\) durch eine monoton steigende Kurve verbunden werden können. Der zweite Beweisweg liefert auch noch weitere Aussagen über die lokale Interner Zinsfaktor-Funktion.
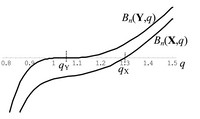
Abb. 2 Die Graphen der Barwertfunktionen Bn(X,q) und Bn(Y,q) der direkt vergleichbaren NU-Finanzierungen X und Y mit D = X - Y \(\underset{\cdot}{<}\) O und den internen Zinsfaktoren qX = qint(X) > qY = qint(Y)
Literatur
Pleier R. (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage.