Dr. Dr. Rudolf Pleier

Die Duplizierung und Replizierung zur Beurteilung von sicheren diskreten Zahlungsströmen bei unvollkommenem Kapitalmarkt

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

Die Beurteilung der Zahlungsströme X des ℝⁿ⁺¹ mit den klassischen Methoden (Kapitalwert- bzw. Barwert-, Endwert-, Zeitwert- und Annuitätenmethode) unter Verwendung eines für die Zeitintervalle [k-1,k] (k = 1,…,n) konstanten Kalkulationszinsfaktors q = q_K > 0 erfolgt unter der impliziten Prämisse, dass für den Entscheider die Ergänzungsgeschäfte des speziellen vollkommenen Kapitalmarkts

                        K = H_P,0 = [P]^⊥ = {X ∈ ℝⁿ⁺¹ : P^TX = 0},

mit dem Preisvektor

                        P = P(q) = (1,1/q,…,1/qⁿ)^T, q = q_K,

zur Verfügung stehen (Pleier 2021, S. 258). Die oben angegebenen Methoden liefern alle die gleiche Präferenzordnung ⊵, die beispielsweise mit der speziellen Barwertfunktion

                        B_n(X) = P(q)^TX = X₀ + X₁/q + ... + X_n/qⁿ  

als Nutzenfunktion beschrieben werden kann.

Etwas allgemeiner beinhaltet die Voraussetzung eines vollkommenen Kapitalmarkts K, der noch vollständig[1] und arbitragefrei[2] sei, auch die Existenz eines positiven Preisvektors[3]

                        P = (d₀,d₁,…,d_n)^T ∈ K^⊥ mit P > O und P₀ = d₀ = 1,    

so dass auch hier K = H_P,0 ist und die Beurteilung der Zahlungsströme X ∈ ℝⁿ⁺¹ mit der Bar­wertfunktion

                        B_n(X) = P^TX = X₀ + d₁X₁ + ... + d_nX_n 

als Nutzenfunktion erfolgen kann. Der Fall eines vollkommenen Kapitalmarkts ist bei den nachfolgenden Überlegungen als Spezialfall mit enthalten.

Um auch für den Fall eines unvollkommenen Kapitalmarkts mit der Berücksichtigung der Geld-Brief-Differenz (bid-ask-spread, bid-offer-spread) zwischen Geldkurs und Briefkurs der Finanzmarktinstrumente eine Beurteilung der Zahlungsströme bereitzustellen, gibt es in der Literatur eine Reihe von Ansätzen für die Konzepte der Duplizierung (Nachbil­dung, Syntheti­sierung, additiven Zerlegung) und der Replizierung (Glattstellung, additiven Ergänzung): Fisher (1932), S. 109–120, Heister (1962), S. 36–60, Kruschwitz (1978), S. 47–95, Marusev (1988), S. 59–60, Locarek (1992), 79–81, Kober, Knöll und Rometsch (1992), S. 129–140, 142–149, Eisenführ (1993), S. 118, Uhlir und Steiner (1994), S. 34–37, Sievi (1995), S. 77–85, Grob (1999), S. 91–95, 102–103, 105–106. Diese verschiedenen Varianten werden in der Komponenten­schreibweise oder als Ta­bellenkalkulation angegeben und unterscheiden sich in der Berücksichtigung des Basiszah­lungsstroms, der Auswahl der ergänzenden Kapitalmarktgeschäfte und der Wahl der Zielset­zung. Nachfolgend wird nun für die beiden Konzepte jeweils eine ziemlich allgemeine Defi­nition in der Vektorschreibweise dargestellt.        

 

---

[1] Die Vollständigkeit des Kapitalmarkts K sei hier gemäß Kruschwitz (1999), S. 77, definiert und bedeutet dim K = n.  

[2] Die Arbitragefreiheit von K bedeutet, dass es in K kein Kapitalmarktgeschäft S mit S 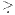 O, d. h. S ≥ O  und S ≠ O, gibt.

[3] Die Existenz eines positiven Normalenvektors P von K folgt mit einem Alternativsatz über die Disjunktheit punktierter konvexer Kegel, der im Spezialfall eines linearen Unterraums K dem Alternativsatz von Stiemke über die Lösbarkeit von homogenen linearen Ungleichungssystemen entspricht.  

 

Um für die Zahlungsströme X des ℝⁿ⁺¹ mit Hilfe der Konzepte der Duplizierung und der Replizierung  jeweils eine (n + 1)-dimensionale Präferenzfunktion (Beurteilungsfunktion) zu konstruieren, wird als Erstes eine geeignete Beurteilungskurve (Präferenzkurve, Zielsetzungskurve) bereitgestellt, die mit einer (Total-)Ordnung versehen ist. Die Beurteilungskurve beschreibt die Zielsetzung des Entscheiders im Sinne einer standardisierten Festlegung der Zeitpräferenz und präzisiert, wie der Entscheider in Abhängigkeit von einem reellen Parameter μ ∈ J die bei der Duplizierung bzw. Replizierung des Zahlungsstroms auftretende Marge (Spanne, Differenz) als Margenzahlungsstrom (Differenzzahlungsstrom) W(μ) in n + 1 Komponenten W_j(μ) auf die Zahlungszeitpunkte j = 0,1,…,n verteilen will. Die Beurteilungskurve W im ℝⁿ⁺¹ wird als eine Äquivalenzklasse von Parameterdarstellungen definiert. Dabei ist eine Parameterdarstellung von W eine stetige Abbildung

eines offenen Intervalls J =]a,b[, -∞ ≤ a < 0 < b ≤ +∞, in den Raum ℝⁿ⁺¹. Weiter wird für eine Parameterdarstellung W(μ) von W gefordert, dass sie bezüglich der strengen Halbordnung 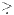(≥∩≠) des ℝⁿ⁺¹ streng monoton steigend ist:

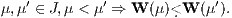
Für zwei Zahlungsströme X, Y ∈ ℝⁿ⁺¹ ist die Relation X 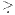Y definiert durch X ≥ Y und X ≠ Y. Jede derartige sogenannte inhomogene Beurteilungskurve W(μ) setzt sich additiv zusammen aus dem festen Bezugspunkt U := W(0) ∈ ℝⁿ⁺¹ und der sog. homogenen Beurteilungskurve V(μ) := W(μ) - U, die ebenfalls stetig und bezüglich der strengen Halbordnung 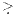streng monoton steigend ist und die außerdem noch durch den Nullpunkt verläuft (V(0) = O):

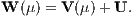
Eine homogene Beurteilungskurve V(μ) ist in Abbildung 1 dargestellt. Alle Kurvenpunkte der homogenen Beurteilungskurve V(μ) sind direkt beurteilbar, d. h. mit O vergleichbar:

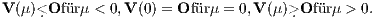
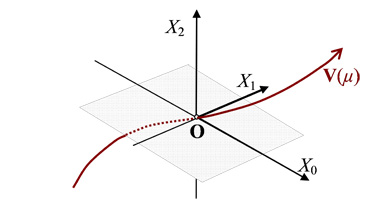
Abb. 1 Eine homogene Beurteilungskurve V(μ) für die Laufzeit n = 2

Für den Nachweis der Existenz und Einzigkeit der Duplizierung und Replizierung bei Verwendung des vollkommenen Kapitalmarkts oder eines speziellen Supplementsystems des unvollkommenen Kapitalmarkts wird noch die Unbeschränktheit der Beurteilungskurve an den Intervallgrenzen von J gefordert:

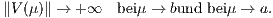
Einfache Beispiele für homogene Beurteilungskurven V(µ) sind die li­ne­aren Be­ur­tei­lungskur­ven

                        V(µ) = µ·A,  A 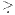 O, µ ∈ J = ℝ,

und Spezial­fälle hiervon die Be­urtei­lungs­­kur­ve  V(µ) = (0,…,0,µ)^T der Endentnahme, die Beurteilungskurve V(µ) = (µ,0,…,0)^T der Sofort­ent­nahme und die Beurteilungskurve V(µ) = (0,µ,…, µ)^T der Annuitätenentnahme mit der konstanten Annuität µ zu den Zeitpunkten j = 1,…,n.

Zwei Parameterdarstellungen W : J → ℝⁿ⁺¹ und W^* : J^* → ℝⁿ⁺¹ heißen hierbei äquivalent, wenn es eine Parametertransformation als streng monoton steigende, surjektive und stetige Funktion g : J^* → J gibt, so dass W^* die Zusammensetzung W ∘ g der Funktionen g und W ist:

Zwei Beurteilungskurven W und W^* sind als Äquivalenzklassen genau dann gleich, wenn für ihre Parameterdarstellungen W(μ) und W^*(μ^*) die Spuren (Bildmengen) W(J) und W^*(J^*) übereinstimmen (Pleier 2021, S. 405).

 

Als Zweites wird für die beiden Konzepte der im Allgemeinen unvollkommene Kapitalmarkt K ⊊ ℝⁿ⁺¹ (i. A. -K ⊈ K) als konvexer linearer Kegel und als arbitragefrei (K ∩ ℝⁿ⁺¹₊₀ = O) vorausgesetzt, so dass nach dem Alternativsatz für punktierte konvexe Kegel für den Linienraum V := K ∩ (-K) von K ein positiver Normalenvektor P ∈ V^⊥ (P₀ = 1) existiert. Im Kapitalmarkt K wird ein Supplementsystem L vorausgesetzt, aus dem die zulässige Supplementmenge C_Mⁿ gebildet wird. Die Kapitalmarktgeschäfte von C_Mⁿ sollen dem Entscheider zur Verfügung stehen und bei der Duplizierung bzw. Replizierung als Ergänzungsgeschäfte (Supplemente) dienen, um jedem Zahlungsstrom X ∈ ℝⁿ⁺¹ genau einen beurteilbaren (i.S.v. mit U = W(0) vergleichbaren) und mit anderen Margenzahlungsströmen vergleichbaren Margenzahlungsstrom W(μ(X)) auf der Beurteilungskurve zuzuordnen. Bei unvollkommenem Kapitalmarkt setzt sich das Supplementsystem L aus n linear unabhängigen Investitionen (lexikonegativen Zahlungsströmen)

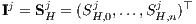
und n linear unabhängigen Finanzierungen (lexikopositiven Zahlungsströmen)

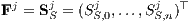
(j = 1,…,n) des Kapitalmarkts zusammen:

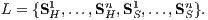
Dabei soll auch jedes n-Tupel

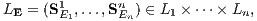
L_j =  {S_H^j,S_S^j}, E =  (E₁,…,E_n) ∈  Mⁿ, M = {H,S}, linear unabhängig sein. Die zulässige Supplementmenge C_Mⁿ wird als der lineare Kegel definiert, der durch die Vereinigung der konvexen linearen Kegel C_E = cone L_E, der so genannten Transformationskegel (Transaktionskegel), gebildet wird:

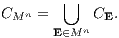
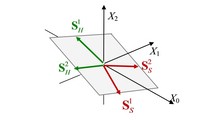
Dieser spezielle Ansatz für die zulässige Supplementmenge beinhaltet das auch bei Kruschwitz (1998), S. 57, verwendete Verbot der gleichzeitigen Durchführung einer Ergänzungsinvestition und einer Ergänzungsfinanzierung. Die Abbildung 2 zeigt für die Laufzeit n = 2 die zulässige Supplementmenge als Ebene bei vollkommenem Kapitalmarkt und als geknickte Ebene bei unvollkommenem Kapitalmarkt.

a)

b)

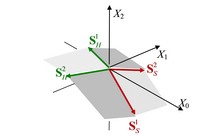Abb. 2 Das Supplementsystem L = {S_H¹,S_H²,S_S¹,S_S²} und die zulässige Supplementmenge C_M² = C_(H,H) ∪ C_(H,S) ∪ C_(S,H) ∪ C_(S,S) bei a) vollkommenem und b) unvollkommenem Kapitalmarkt für die Laufzeit n = 2

 

Als Drittes wird vom Supplementsystem L noch verlangt, dass für jede beliebig fest vorgegebene Beurteilungskurve W(μ) und für jeden Zahlungsstrom X ∈ ℝⁿ⁺¹ die Duplizierung bzw. die Replizierung auf genau eine Weise möglich ist: Bei der Duplizierung eines beliebigen Zahlungsstroms X ∈ ℝⁿ⁺¹,

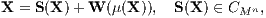
und bei der Replizierung von X ∈ ℝⁿ⁺¹,

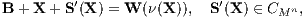
mit der Beurteilungskurve W(μ) zur Beschreibung der zeitlichen Zielsetzung des Entscheiders, dem Basiszahlungsstrom B zur Beschreibung der situativen Liquidität des Entscheiders und dem für S(X) bzw. S′(X) verwendeten Supplementansatz

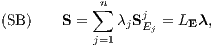
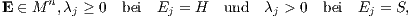
sind dann also jeweils die Parameter E = E(X) ∈ Mⁿ, μ(X) bzw. ν(X) ∈ J und λ = λ(X) \(\in \mathbb{R}^{n}_{\geq 0}\), das Supplement S = L_Eλ und der Margenzahlungsstrom W(μ(X)) bzw. W(ν(X)) eindeutig bestimmt.

 

Auf der Grundlage der eindeutigen Duplizierung bzw. Replizierung erhält man auf ℝⁿ⁺¹ eine D-Präferenzordnung ⊵_DW und eine R-Präferenzordnung ⊵_RW. 

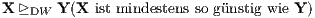
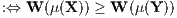
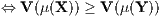
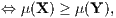
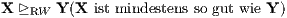
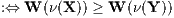
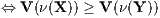
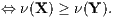
Außerdem erhält man die (n + 1)-dimensionalen Präferenzfunktionen (Bewertungsfunktionen)

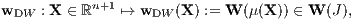
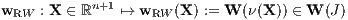
und die ordinalen Nutzenfunktionen (eindimensionalen Bewertungsfunktionen)

Die Abbildung 3 zeigt die Funktionswerte der D- und R-Präferenzfunktion auf der Beurteilungskurve.  Im Thema ‚Die eindeutige Duplizierung und Replizierung mit speziellen Supplement­systemen‘ wird dargestellt, dass bei bestimmten Klassen von Supplementsystemen des unvollkommenen Kapitalmarkts die Berechnung des Beurteilungsparameters μ_DW(X) bzw. ν_RW(X) durch die iterative Nullstellenbestimmung für eine streng monotone stetige Hilfsfunktion erfolgen kann.

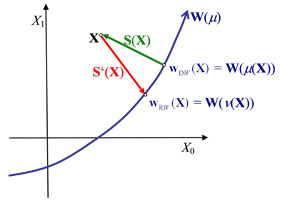
Abb. 3 Die Werte der D-Präferenzfunktion w_DW(X) und R-Präferenzfunktion w_RW(X) auf der Beurteilungskurve W(μ) (B = O, n = 1)

In der Abbildung 4 sind die Bessermengen

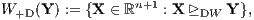
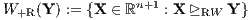
eines Zahlungsstroms Y ∈ ℝⁿ⁺¹ bezüglich der D-Präferenzordnung ⊵_DW und der R-Präferenzordnung ⊵_RW bei gleicher Beurteilungskurve W(μ) dargestellt. Die Vielfalt der D- und R-Präferenzordnungen in Abhängigkeit vom Supplementsystem L und von der Beurteilungskurve W(μ) werden im Thema ‚Die Vielfalt der Präferenzordnungen nach den Konzepten der Duplizierung und Replizierung‘ beschrieben.  

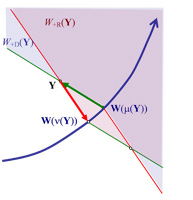
Abb. 4 Die Bessermengen W_+D(Y) und W_+R(Y) eines Zahlungsstroms Y ∈ ℝ² (B = O, n = 1)

 

In einem einfachen Beispiel „Robinson auf dem Kartoffelmarkt“ für einen unvollkommenen Kapitalmarkt werden bei Pleier (2021), S. 35-57, die durch die Konzepte der Duplizierung und Replizierung gewonnenen Präferenzordnungen verglichen.

Abb. 5 Robinson auf dem Kartoffelmarkt       

Wie eine Entscheidung mit den beiden genannten Konzepten zustande kommen kann, wenn kein Kapitalmarkt zur Verfügung steht, wird bei Pleier (2021), S. 11-34, in einem einfachen Beispiel „Robinson beim Fischfang" dargestellt, in dem Robinson die zwei Alternativen "Fischfang heute mit Speer" oder "Fischfang morgen mit Netz" zur Wahl hat.  

a) Fischfang mit Speer

b) Fischfang mit Netz

Abb. 6 Robinson beim Fischfang          

 

Im Spezialfall eines vollkommenen Kapitalmarkts

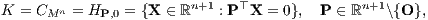
liefert jedes n-Tupel L_E = (S_E1¹,…,S_Enⁿ), E ∈ Mⁿ, eine Basis S = L_E der Hyperebene K von ℝⁿ⁺¹. Umgekehrt erhält man auch aus einer Basis S =  {S¹,…,Sⁿ} der Hyperebene K des ℝⁿ⁺¹ mit L = {±S¹,…,±Sⁿ} ein Supplementsystem L. Bei arbitragefreiem Kapitalmarkt K kann nach dem Alternativsatz der konvexen Geometrie über die Disjunktheit punktierter konvexer Kegel der Normalenvektor P der Hyperebene H_P,0 (strikt) positiv gewählt werden. Der mit P₀ = 1 normierte Normalenvektor P heißt Preisvektor des vollkommenen Kapitalmarkts. Mit der streng monoton steigenden „Abstandsfunktion“ α(μ) = P^⊤V(μ) erhält man die Beurteilungsparameter von X durch

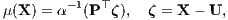
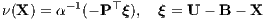
und somit die Margenzahlungsströme W(μ(X)) und W(ν(X)), ohne die Supplemente S(X) und S′(X) berechnen zu müssen. Die Berechnung des Beurteilungsparameters μ(X) bzw. ν(X) erfolgt dabei im Allgemeinen mit einer iterativen Nullstellenbestimmung für die Funktion f(μ) := α(μ) - P^⊤ζ bzw. g(ν) := α(ν) + P^⊤ξ. In diesem Spezialfall stimmen für jede Beurteilungskurve W(μ) die D- und die R-Präferenzordnung mit der Barwert-Präferenzordnung (B-Präferenzordnung) ⊵ überein, so dass der Vergleich zweier Zahlungsströme X, Y ∈ ℝⁿ⁺¹ auch unabhängig von der Beurteilungskurve mit der Barwertfunktion B_n(X) = P^TX als Nutzenfunktion erfolgen kann:

                     X ⊵ Y (X ist mindestens so vorteilhaft wie Y) ⇔ B_n(X) ≥ B_n(Y).   

 

Literatur

Eisenführ F. (1993), Beurteilungskriterien für Investitions- und Finanzierungs­alterna­ti­ven bei gegebenen Kapitalkosten, in Gebhart G., Gerke W., Steiner M. (HBF 1993), S. 99–119.

Fisher I. (1932), Die Zinstheorie, Deutsche Übersetzung von H. Schulz, Gustav Fischer Verlag, Jena.

Grob H. L. (1999), Einführung in die Investitionsrechnung, Vahlen Ver­lag, München, 3. Auflage.

Heister M. (1962), Rentabilitätsanalyse von Investitionen, Westdeutscher Verlag, Köln Opladen.

Kober J., Knöll H.-D., Rometsch U. (1992), Finanzmathematische Ef­fektivzins-Berech­nungs­metho­den, BI-Wissenschaftsverlag, Mannheim Leipzig Wien Zürich.

Kruschwitz L. (1978), Investitionsrechnung, de Gruyter Verlag, Berlin New York, 1. Auflage.

Kruschwitz L. (1999), Finanzierung und Investition, Oldenbourg Verlag, München Wien, 2. Auflage.

Kruschwitz L. (1998), Investitionsrechnung, Oldenbourg Verlag, München Wien, Boston, 7. Auflage.

Locarek H. (1992), Finanzmathematik, Oldenbourg Verlag, München Wien, 2. Auflage.

Marusev A. W. (1988), Die Marktzinsmethode im Tagesgeschäft der Banken. In: Schierenbeck, Schimmelmann, Rolfes (Hrsg), Bank‑Controlling 1988, Fritz Knapp Verlag, Frankfurt am Main, S. 59–68.

Pleier R. (2021), Finanzmathematik, Tredition, Hamburg, 2. Auflage.

Sievi Ch. (1995), Kalkulation und Disposition, Gillardon Verlag, Bretten.

Uhlir H., Steiner P. (1994), Wertpapieranalyse, Physika Verlag, Heidel­berg, 3. Auflage.