Dr. Dr. Rudolf Pleier

Das Mehrperiodenmodell zur Bewertung unsicherer zeitdiskreter Zahlungsströme bei vollkommenem Kapitalmarkt

⇒ Das Thema als PDF zum Download

Rudolf Pleier
Juni 2015

Zur Formulierung von Aussagen zur Bewertung nach dem Duplikationsprinzip im Mehrperiodenmodell und zu den zentralen Begriffen Gesetz des eindeutig bestimmten Preises, Arbitragefreiheit und Vollständigkeit des Marktmodells sind zunächst Begriffe zur Beschreibung des zeitdiskreten Marktmodells, bei T = 1 des Einperiodenmodells (englisch: one period model) und bei T > 1 des Mehrperiodenmodells (englisch: multi-period model), vorzustellen.

Für das Marktmodell werden N Finanzinstrumente (Wertpapiere) S^j ausgewählt und die endlich vielen Kursentwicklungen des zugehörigen Preisvektors

über der Zeitparametermenge I = {0,…,T} mathematisch modelliert. Die Kursentwicklungen liefern den endlichen Zustandsraum Ω = {ω₁,…,ω_K}  (|Ω| = K), so dass der Preisvektor S = (S¹,…,S^N)^T ein N-dimensionaler stochastischer Prozess über I x Ω ist. Neben dem Preisprozess S wird noch ein Dividendenprozess δ und der kombinierte Prozess S^δ=S+ δ betrachtet.  Der im Zeitverlauf stattfindende Wissenszuwachs über den Preisprozess S wird durch die zugehörige natürliche Filtration 𝒫 = (𝒫_t)_t∈I von Partitionen 𝒫_t = {A_t,1,…,A_t,kt} (k ∈ I, 𝒫₀ = {Ω}, 𝒫_T = {{ω₁},…,{ω_K}}) von Ω bzw. die Filtration ℱ = (ℱ_t)_t∈I von σ-Algebren  ℱ_t =σ(𝒫_t) über Ω beschrieben. Damit liegt der Preisprozess S im Untervektorraum 𝒲_N = 𝒲_N (ℱ) der  ℱ-adaptierten ℝ^N-wertigen stochastischen Prozesse

 

deren Zustandsfunktionen X_t  ℱ_t-messbar sind. Für die Eintrittswahrscheinlichkeiten P({ω}) der Kursentwicklungen ω ∈ Ω kann o. B. d. A. deren Positivität vorausgesetzt werden. Es wird sich zeigen, dass diese bei der im Mehrperiodenmodell erfolgenden Bewertung von Zahlungsströmen gar nicht benötigt werden. Zur Beschreibung eines Portfolios der N Wertpapiere S^j werden sog. Handelsstrategien verwendet, d. h. ℱ-vorhersehbare Handelsprozesse h, deren Zustandsfunktionen h_t  ℱ_t-1-messbar sind. Deren Gesamtheit bildet den in 𝒲_N  gelegenen Unterraum ℋ_N = ℋ_N (ℱ). Zur Präzisierung der zeitlichen Entwicklung des zur Handelsstrategie h gehörigen Portfoliowertes dienen der Vermögensprozess V(h) = S^δh, der durch die Zustandsfunktionen R_t(h) = S_th_t+1 (t ∈ I) definierte Reinvestitionsprozess R(h) und das (Aus)Zahlungsprofil

 

Zur Bewertung mittels des Marktmodells sind nur Zahlungsströme

im Vektorraum 𝒲 = 𝒲₁(ℱ) der ℱ-adaptierten reellwertigen stochastischen Prozesse zugelassen. Außerdem soll die Bewertung nach dem Duplikationsprinzip erfolgen, bei dem das zu bewertende Zahlungsprofil X ∈ 𝒲 als das Zahlungsprofil L(h) einer Handelsstrategie h ∈ ℋ_N dupliziert (nachgebildet, erreicht) werden kann: Die Übereinstimmung der beiden Zahlungsprofile X und L(h) soll dabei für alle t ∈ I und ω ∈ Ω gelten, also insbesondere sicher bezüglich der Eintrittswahrscheinlichkeiten P(ω) der Kursentwicklungen ω ∈ Ω. Eine Duplikationsstrategie h ∈ L^-1({X}) von X kann dann sicher und linearalgebraisch (also nicht wahrscheinlichkeitstheoretisch) durch das Lösen des gestaffelten inhomogenen linearen Gleichungssystems

bestimmt werden. Eine ausführlichere Darstellung des linearen Gleichungssystems (DP) findet man beim Thema „Die Duplikation als Zahlungsprofil einer Handelsstrategie zur Beurteilung unsicherer diskreter Zah­lungs­ströme“. Falls noch der Portfoliowert V₀(h) bei t = 0 für alle Duplikationsstrategien h von X konstant ist, kann der Preis π(X) von X bzw. der Wert von X zum Zeitpunkt t = 0 durch den deterministischen Startkapitaleinsatz V₀(h) = S₀^δ(Ω)^⊤h₀(Ω) der Handelsstrategie h zum Zeitpunkt t = 0 definiert werden:

Falls nun diese Eigenschaft zumindest für ein X ∈ L(ℋ_N) erfüllt ist, so kann gezeigt werden, dass sie dann auch für alle X ∈ L(ℋ_N) vorliegt. Im Unterraum L(ℋ_N) (⊆ 𝒲) des Marktmodells ((S,δ),ℱ) gilt dann das sogenannte Gesetz des eindeutig bestimmten Preises (englisch: Law of One Price, Abk.: LOP) und alle X ∈ L(ℋ_N) können mit der Nutzenfunktion π(X) bewertet und verglichen werden:

Aufgrund der für eine Duplikationsstrategie h von X gültigen Beziehung

   S₀^δ⊤h₀ = V₀(h) = X₀ + R₀(h)= X₀ + S₀^⊤h₁

ist die Bedingung (LOP) äquivalent zur Bedingung

Bei gültigem LOP kann also jedes duplizierbare Zahlungsprofil X ∈ L(ℋ_N) durch den für seine Dupli­kationsstrategien h ∈ L^-1({X}) konstanten Wert V₀(h) =: π(X) des Startkapitaleinsatzes, den Preis von X, bewertet werden. Diese Bewertung von X ist aufgrund der P-sicheren Defini­tion der Duplikation mittels einer Handelsstrategie h und wegen der deterministischen Berech­nung des Werts V₀(h) = S₀^δ⊤h₀ einer Duplikationsstrategie h bzw. des Preises π(X) von X linearal­gebraisch und nicht wahrscheinlichkeitstheoretisch. Es handelt sich hierbei außerdem um einen relativen Bewertungsansatz wegen der speziellen Auswahl der zugrunde gelegten Wertpapiere S ^j (j = 1,…,N) und der Einschränkung der Bewertung auf Zahlungspro­file X ∈ L(ℋ_N) ⊆ 𝒲(ℱ), die mittels (ℱ-vor­hersehbarer) Handelsstrategien dupli­zier­bar sind.           

Das Marktmodell heißt vollständig (englisch: complete market model), wenn jedes Zahlungsprofil X ∈ 𝒲 durch eine Handelsstrategie h ∈ ℋ_N duplizierbar ist, wenn also das Bild L(ℋ_N) der Abbildung L den gesamten Zielraum 𝒲 ausfüllt:

 

Weiter gilt im Marktmodell ((S,δ),ℱ) die Arbitragefreiheit (englisch: No-Arbitrage Principle, Arbitrage-Free Condition), wenn es keine Arbitragegelegenheit h ∈ ℋ_N, d. h. keine Handelsstrategie h ohne Startkapitaleinsatz (V₀(h)= 0) und dennoch mit schwach positivem Zahlungsprofil L(h) gibt:

  

Dabei bedeutet L(h) 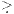0, dass L_t(h)(ω) ≥ 0 für alle (t,ω) ∈ I × Ω und L_t'(h)(ω') > 0 für mindestens ein Paar (t',ω') ∈ I × Ω gilt.

 

Für die Vektorräume ℋ_N und 𝒲 wird jeweils mit einer endlichen Basis (h_t,At-1,j = 1_t,At-1,j ∈ ℋ_N, t ∈ I, A_t-1 ∈ 𝒫_t-1, j ∈ J = {1,…,N}  bzw.  w_t,At = 1_t,At ∈ 𝒲, t ∈ I, A_t ∈ 𝒫_t) die Isomorphie zu einem passenden ℝⁿ gezeigt. Demzufolge können die Handelsstrategien h ∈ ℋ_N und die Zahlungsprofile X ∈ 𝒲 auch mit den zugehörigen Koordinaten-Tupeln identifiziert werden. Außerdem können diese Vektorräume jeweils mit einem Skalarprodukt

 

ausgestattet werden, das mit dem Standardskalarprodukt der Koordinaten-Tupel übereinstimmt. Beispielsweise erhält man dann mit der deterministischen Handelsstrategie

b = (S₀^δ)_0,Ω ∈ ℋ_N,

die für t = 0 den Wert S₀^δ(Ω) und für t = 1,…,T den Wert Null annimmt, den Portfoliowert V₀(h) als das Skalarprodukt der Handelsstrategien b und h bzw. der zugehörigen Koordinaten-Tupel b und h:

 

Mit der zu diesem Bewertungsprozess b ∈ ℋ_N gehörigen Nutzenfunktion V₀(h) = b^⊤h können alle Handelsstrategien h ∈ ℋ_N bewertet und verglichen werden.

Da der Vektorraum ℋ_N eine endliche Dimension besitzt, existiert zur linearen Abbildung L : ℋ_N → 𝒲 auch die eindeutig bestimmte adjungierte Abbildung L* : 𝒲 → ℋ_N mit der definierenden Eigenschaft

Mit den Bildräumen und Kernen der linearen Abbildungen L und L* lassen sich die Vektorräume ℋ_N und 𝒲 als direkte Summen von orthogonalen Komplementen darstellen:

Weiter existiert für die lineare Abbildung L die additive Zerlegung

in deterministischen Anteil 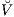(h) = V₀(h)1_0,Ω  (1_0,Ω ∈ 𝒲 ist gleich 1 für t = 0 und gleich 0 für t > 0) und stochastischen Anteil 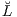(h). Entsprechend gilt für die adjungierte Abbildung

 

mit deterministischem Anteil und stochastischem Anteil  

 

1  Charakterisierungen der Begriffe Duplizierbarkeit, Vollständigkeit, Law of One Price und Arbitragefreiheit

Zur Formulierung verschiedener Charakterisierungen der oben genannten Begriffe in der nachfolgenden Tabelle 1 werden noch folgende Unterräume von ℋ_N bzw. 𝒲 und Orthanten von 𝒲 benötigt:

         

Die dabei auftretenden stochastischen Prozesse Ψ, Φ ∈ ℳ^⊥\ ker L* ⊆ 𝒲 mit Ψ₀ = 1 und Φ₀ = 1 werden als Bewertungsprozess bzw. Diskontierungsprozess oder Zustands(preis)prozess bezeichnet. Bei den Charakterisierungen des Law of One Price und der Arbitragefreiheit werden nachfolgend nicht nur lineare Gleichungen für die h ∈ ℋ_N bzw. h ∈ ker V₀ = ℬ^⊥, sondern auch Lagebeziehungen für bestimmte Unterräume von ℋ_N und 𝒲 angegeben.

 

Tab. 1 Die Charakterisierungen der Duplizierbarkeit, der Vollständigkeit, des Law of One Price und der Arbitragefreiheit beim Mehrperiodenmodell (m = dim ℋ_N, n₁ = dim 𝒲)

Duplizierbarkeit (DP)
Vollständigkeit (VS)
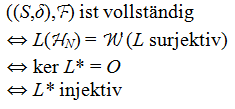Law of One Price (LOP)
LOP nicht gültig
(VS) ∧ LOP
(VS) ∧ m = n1
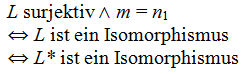(VS) ∧ LOP ungültig
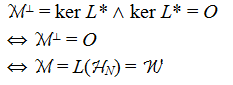Arbitragefreiheit (AF)
(VS) ∧ (AF)

Die Charakterisierung des LOP durch die Preisgleichungen Ψ^⊤L(h) = V₀(h), h ∈ ℋ_N, mit einem Ψ ∈ 𝒲 findet man bei Kremer (2011), S. 171, wobei dort V₀(h) = S₀^δ⊤h₀ und noch nicht die Darstellung V₀(h) = b^⊤h verwendet wird. Die Charakterisierung der Arbitragefreiheit durch die Preisgleichungen Φ^⊤L(h) = V₀(h), h ∈ ℋ_N  bzw. h ∈ ker V₀, mit einem positiven Φ ∈ 𝒲 findet man bei Kremer (2011), S. 175, 176, mit V₀(h) = S₀^δ⊤h₀ und noch ohne die Darstellung V₀(h) = b^⊤h.  

Der Vorteil der neuen Charakterisierungen mittels der Struktur und Lagebeziehungen von Vektorunterräumen besteht nun darin, dass sie geometrisch visualisiert werden können. Andererseits kann die geome­tri­sche Veranschaulichung auch als Quelle für Vermutungen über weitere neue Erkennt­nisse dienen. Beispielsweise lässt sich der Vektorraum 𝒲 der ℱ-adaptierten stochastischen Prozesse darstellen als direkte Summe der Unterräume L(ℋ_N) und ker L* und als direkte Summe von ℳ und ℳ^⊥. Dabei liegt stets ℳ in L(ℋ_N) und ker L* in ℳ^⊥. In der Abbildung 2 ist dargestellt, dass bei ungültigem LOP sowohl der Unterraum ℳ der Kapitalmarktgeschäfte mit dem Unterraum L(ℋ_N) der duplizierbaren Zahlungsströme als auch der Unterraum ℳ^⊥ mit dem Unterraum ker L* zusammenfällt. In der Abbildung 1 sieht man dagegen, dass mit der Einstellung des LOP im Marktmodell der Unterraum ℳ um eine Dimension kleiner ausfällt als der Unterraum  L(ℋ_N) und der Unterraum ℳ^⊥ um eine Dimension größer wird als ker L*. Im nichtleeren Bereich ℳ^⊥ \ ker L* liegt dann der Bewertungsprozess Ψ (Ψ₀ = 1), mit dem der Preis π(X) eines duplizierbaren Zahlungsprofils X ∈ L(ℋ_N) als Skalarprodukt

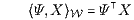
und somit unabhängig von einer Duplikationsstrategie berechnet werden kann: Für diesen Pro­zess Ψ gilt nämlich L*(Ψ) = b, sodass für ein festes Zahlungsprofil X ∈ L(ℋ_N) alle Duplikations­strategien h von X bei Verwendung der deterministischen linearen Nutzenfunktion

                                   V₀(h) = b^⊤h,

die h durch den deterministischen Startkapitaleinsatz zum Zeitpunkt t = 0 beurteilt, mit dem glei­chen Wert

                                   b^⊤h = L*(Ψ)^Th = Ψ^TL(h) = Ψ^TX 

bewertet werden. Demzufolge kann der Startkapital­einsatz V₀(h) = b^⊤h einer beliebi­gen Duplikations­strate­gie h von X dann auch zur Bewertung von X und die Linearform π(X) = Ψ^TX  als lineare Nutzenfunktion auf L(ℋ_N) verwendet werden.

Bei gleichzeitigem Vorliegen der Voraussetzungen (LOP) und (VS) existiert genau eine Linearform π = Ψ^T auf 𝒲, die auf L(ℋ_N) gemäß den Gleichungen (PGΨ) die Preise liefert. Bei gleichzeitiger Gültigkeit von (AF) und (VS) existiert genau eine Linearform π = Φ^T auf 𝒲, die auf L(ℋ_N) gemäß den Gleichungen (PGΦ) die Preise liefert, und diese Linearform ist noch eine sog. positive Linearform (π(X) > 0 für alle X ∈ ).

Bei diesen Betrachtungen stellt sich auch die Frage, ob die hier für das zeitdiskrete Marktmodell angegebenen geometrischen Charakterisierungen von (LOP), (AF) und (VS) auch ein Analogon im zeitkontinuierlichen Marktmodell aufweisen. 

Beweise für die Charakterisierungen des LOP und der Arbitragefreiheit findet man in der pdf-Datei zu diesem Thema.

 

Abb. 1 Die verschiedenen Unterräume von ℋ_N und 𝒲, die linearen Abbildungen L, L* und π, der Bewertungsprozess Ψ bei gültigem LOP und der Zustandspreisprozess Φ bei Arbitragefreiheit

Abb. 2 Die verschiedenen Unterräume von ℋ_N und 𝒲 und die linearen Abbildungen L und L* bei nicht gültigem LOP

 

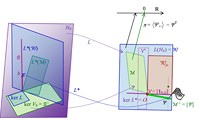
Abb. 3 Die verschiedenen Unterräume von ℋ_N und 𝒲, die linearen Abbildungen L, L*, π und der Bewertungsprozess Ψ bei vollständigem Marktmodell und gültigem LOP



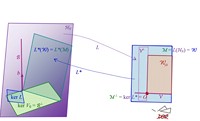
Abb. 4 Die verschiedenen Unterräume von ℋ_N und 𝒲 und die linearen Abbildungen L und L* bei vollständigem Marktmodell und ungültigem LOP

 

2  Formales Wahrscheinlichkeitsmaß, Preismaß, Martingalmaß und risikoneutrales Wahr­schein­lich­keitsmaß 

In der zu diesem Thema gehörigen pdf-Datei werden auch noch ei­nige in der Literatur vielzitierte Begriffe im Mehrperioden­modell erläutert. Es sind dies die in der Überschrift aufgeführten Bezeichnungen und außerdem die Begriffe Arrow-Debreu-Preis, Zu­stands­­preis, Er­eignispreis, Arrow-Debreu-Preis­vektor, Zustandspreis­vek­tor, Ereig­nispreis­vek­tor, deterministischer Preisvektor und risikoneutrale Bewertung. Mittels der Dupli­zierbarkeit bestimmter Arrow-Debreu-Papiere (1_t,C, C ∈ ℱ_t = σ(𝒫_t)) werden dabei auch die meist weniger beachteten impliziten Prämissen darge­stellt, unter denen diese Begriffe erst einen Sinn haben. Bei vorliegender Arbitragefreiheit (AF) und unter der Voraussetzung (FH) der Existenz von sog. festverzinsli­chen Han­delsstrate­gien existiert das für alle Zeitpunkte t ∈ I einheitliche formale (synthetische) Wahrscheinlichkeitsmaß Q. Unter diesen Voraussetzungen kann dieses W-Maß Q auch Martingalmaß und risikoloses bzw. risikoneut­rales Wahrschein­lich­keitsmaß genannt werden. Außerdem kann unter diesen Voraussetzungen die Bewertung nach dem Duplikationsprinzip als Barwertberechnung (Diskontierung) mit dem deterministi­schen Preisvektor P := (d₀,…,d_T)^T (d_t = Φ_t(Ω)) für die Q-Erwartungswerte der Zustandsfunktionen X_t be­züg­lich des sog. risi­ko­neutralen W-Maßes Q interpretiert werden und daher risi­ko­neutrale Bewertung genannt werden. Weiter kann das W-Maß Q als Preismaß bezeichnet werden, wenn die Voraussetzungen (AF), (FH) und die Vollständigkeit (VS) des Marktmodells vorliegen.   

Literatur

[1]   Jürgen Kremer (2011), Portfoliotheorie, Risikomanagement und die Bewertung von Derivaten, Springer, Berlin Heidelberg.

[2]   Rudolf Pleier (2023), Diskrete stochastische Finanzmathematik, Tredition. Ahrensburg.